Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 6.Problemas - Ex. 18
Um avião a jato supersônico está voando a Mach 2 (o dobro da velocidade do som). (a) Qual é o ângulo de abertura do cone de Mach? (b) depois de o avião ter passado diretamente acima de uma casa, a onda de choque causada pela sua passagem atinge a casa, provocando um estrondo sônico. A velocidade do som no ar é de . Qual é a altitude do avião em relação à casa?
Passo 1
Se o avião está se movendo mais rápido do que o som, então ele vai ultrapassar as ondas sonoras que saem dele mesmo.
As frentes de onda emitidas em um certo intervalo de tempo estarão contidas em um cone, cujo vértice é o avião:
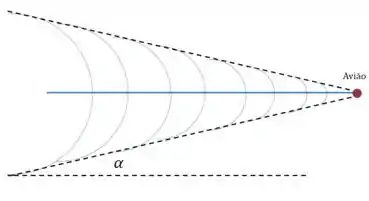
E a fórmula para o ângulo de abertura do cone é:
Onde é a velocidade do som e é a velocidade do avião. Como :
Passo 2
A onda de choque atinge a casa depois de o avião ter passado.
Agora que nós sabemos a abertura do cone de Mach, podemos usar isso para determinar a posição das frentes de onda a partir da velocidade do avião.
No intervalo de , o avião percorre uma distância :
E então:
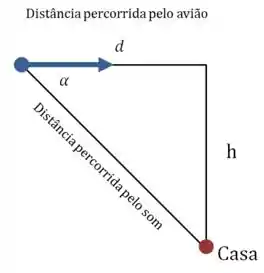
Resposta
(a) O ângulo de abertura é .
(b) A altitude do avião em relação à casa é .