Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 93
Uma barra com área da seção reta A é submetida a forças de dilatação iguais e opostas em suas extremidades. Considere um plano ao longo da barra formando um ângulo com o plano da barra (Figura 11.64).
a) Ache a tensão de dilatação (normal) nesse plano em termos de A, de F e de .
b) Qual é a tensão de cisalhamento (tangencial) no plano em função de A, de F e de ?
c) Para qual valor de a tensão de cisalhamento é máxima?
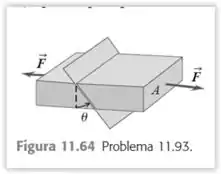
Passo 1
Esse é um caso em que usaremos a tensão de dilatação na seção reta como a razão entre a força e a área A da seção reta
E a tensão de cisalhamento que é a força tangente à superfície de um material, dividida pela área A sobre a qual ela atua:
A tensão de tração depende do componente de perpendicular ao plano e a tensão de cisalhamento depende do componente de paralelo ao plano, como mostra a figura
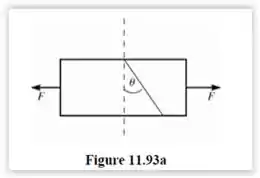
Passo 2
As componentes de são
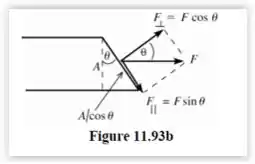
A área da face diagonal é . Sendo assim, teremos que
Passo 3
A tensão de cisalhamento será de
Para que essa tensão de cisalhamento seja máxima, , ou seja, e .
Resposta
a)
b)
c) Para que essa tensão de cisalhamento seja máxima, , ou seja, e .