Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.4 - Ex. 50
Uma barra fina uniforme (massa = 0,50 kg) oscila em torno de um eixo que passa por uma das extremidades da barra e é perpendicular ao plano de oscilação. A barra oscila com um período de 1,5 s e uma amplitude angular de 10º. (a) Qual é o comprimento da barra? Qual é a energia cinética máxima da barra?
Passo 1
Falaa galerinhaa boa, tudo jóinha? Se a gente fizer um desenho da situação em que a barra se encontra, a gente ia ter algo mais ou menos assim:
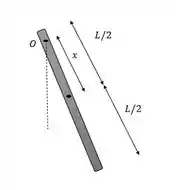
Antes, de tudo, a gente precisa calcular o momento de inércia da barra em torno do seu centro de rotação. Sabendo seu momento de inércia no centro de massa, a gente consegue descobrir o momento de inércia com relação a extremidade usando o teorema dos eixos paralelos. Chamando de a distância entre o centro de rotação e o centro de massa, o teorema dos eixos paralelos fica assim:
Como , obtemos que:
Pronto, agora podemos jogar na equação do período :
Substituindo que foi encontrado e também , vemos que o período é dado como:
Elevando ambos os lados da equação ao quadrado:
Isolando :
Portanto, substituindo os valores que o enunciado nos fornece, descobrimos que:
Passo 2
Pelo princípio da conservação de energia mecânica, a gente sabe que a máxima energia potencial é igual a máxima energia cinética. Assim, como a gente tem o valor da amplitude do movimento, que é , a gente consegue calcular o valor da máxima energia potencial
E substituindo os valores:
Resposta
(a)
(b)