Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 74
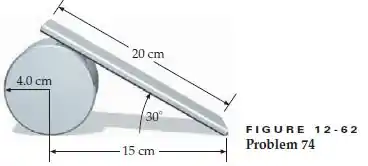
A Figura 12-62 mostra uma prancha homogênea, de 20 cm de comprimento, sobre um cilindro de 4,00 cm de raio. A massa da prancha é 5,0 kg e a do cilindro é 8,0 kg. O coeficiente de atrito estático entre a prancha e o cilindro é zero, enquanto os coeficientes de atrito estático entre o cilindro e o piso, e entre a prancha e o piso, não são nulos. Existem valores, para estes coeficientes de atrito estático, para os quais o sistema fique em equilíbrio estático? Caso afirmativo, que valores são esses? Caso negativo, explique o porquê de sua não existência.
Passo 1
Muito bem gente, nós queremos saber se existe coeficientes de atrito entre o cilindro e o piso e a prancha e o piso capazes de permitir que o sistema fique em equilíbrio estático. Ou seja:
Legal ! Agora vamos desenhar esta situação:
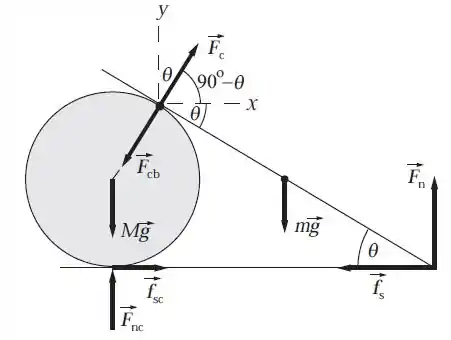
No centro de gravidade, ou seja, no ponto central da prancha e do cilindro, temos a força gravitacional sendo aplicada para baixo. Dada por:
Como nós temos duas superfícies em contato, existe a força norma do chão sobre o cilindro, , a força normal do cilindro na prancha, e da prancha no cilindro (), para finalizar, a força normal do chão sobre a prancha ().
Muito importante aqui é percebermos que são forças de ação e reação:
Ainda temos mais duas forças atuando, a de atrito do chão com o cilindro (,) e da prancha com o chão (,), que são calculados por:
Já definimos todas as forças, então vamos usar as condições do equilíbrio!
Passo 2
Bom, temos que começar optando por usar uma das condições do equilíbrio, neste caso eu vou usar .
O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher a ponta direita da barra, vamos mostrar na figura:
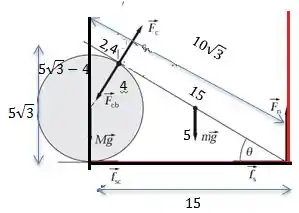
Beleza ! Quando fazemos isso zeramos a força de atrito e a força normal que atuam na barra. A força peso está posição , e a força , está a uma distância Vocês devem se perguntar de onde eu tirei isso, mas se sabemos que o ângulo é 30° e o diâmetro do cilindro é 4 cm, a trigonometria nos ajuda a achar a distância, como está sendo mostrado no desenho !
Já sabemos a distância, agora vamos olhar as forças. Elas devem estar formando um ângulo de 90° com a prancha. A está ok, mas se olharmos para a força peso, ela forma um ângulo de 30° com a sua composição na direção y, ou seja:
Já temos r e as forças perpendiculares, agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força peso é capaz de girar a barra no sentido horário (-), já a normal gira no sentido anti-horário (+).
Jogando toda informação na segunda condição:
Sabemos que:
Então
Do passo 1 sabemos:
Bom, achamos duas forças, mas ainda não conseguimos os coeficientes! Então bora para o passo 3!
Passo 3
Já usamos, uma das condições do equilíbrio para a prancha, agora vamos usar a outra condição ainda para a prancha. Se , então .
Na direção y, temos três forças: , e a componente y de (), então:
Se isolarmos
Substituímos os dados:
Legal, agora vamos para x. Teremos a força de atrito (), e a componente de na direção x ():
Ainda não terminou né galera, mas com isso já achamos um coeficiente de atrito. Pegando as equações lá do passo 1:
Substituímos o que achamos aqui:
Passo 4
Achamos um coeficiente, então já acabou? Não, né?!
Precisamos do coeficiente de atrito entre o cilindro e o chão. Então vamos usar , para o cilindro!
Começando pelo eixo y, nós temos a componente y do , que forma um ângulo de 30° com o eixo y () e, por último a força peso, Mg:
Isolando
Sabemos que:
Na direção x, teremos a força de atrito, , e a componente x de ()
Agora sim, vamos para o último coeficiente:
É isso ai, a situação é possível e já temos os coeficientes !