Um bloco de 2,0 kg é colocado sobre um bloco de 4,0 kg que está sobre uma mesa sem atrito (figura abaixo). Os coeficientes de atrito entre os blocos são e . (a) Qual é a máxima força horizontal que pode ser aplicada ao bloco de 4,0 kg se o bloco de 2,0 kg não deve deslizar? (b) Se tem a metade deste valor, encontre a aceleração de cada bloco e a força de atrito atuando sobre cada bloco. (c) Se tem o dobro do valor encontrado em (a), encontre aceleração de cada bloco.

Passo 1
Letra (a)
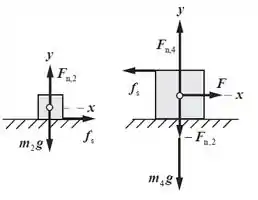
O fato de a força F ser máxima faz com que a força de atrito seja máxima. Vamos para as leis de Newton no bloco de 2 kg:
Joga (1) em (2):
Corta a massa:
Passo 2
Agora vem o pulo do gato. Se o bloco de cima não desliza, então os dois blocos têm a mesma aceleração que a gente achou. Como proceder agora? Faz assim: considera o sistema composto pelas duas massa. Fazendo isso, acontecem duas coisas;
- A força F vai atuar sobre os dois blocos
- A força de atrito vai ser uma força interna, então não vai entrar na conta da lei de Newton:
Joga a (3) na (4):
Agora substitui os valores:
Passo 3
Letra (b)
Se a força tem metade do valor máximo, então ela ainda não é suficiente para que o bloco de cima deslize, então os blocos vão ter a mesma aceleração, como na letra (a). Vamos usar o mesmo pulo do gato para achar a aceleração:
Isola o :
Vamos jogar os valores:
Agora a gente volta pro bloco de cima para calcular a força de atrito:
Passo 4
Letra (c)
Agora o bloco de cima vai deslizar, porque a força é maior do que a máxima. Isto significa que não podemos juntar os blocos num sistema só. Vamos fazer as leis de Newton no bloco de baixo:
Agora em y, só que no bloco de cima:
Passo 5
Aplica (6) em (5):
Isola o :
Só jogar os valores:
Passo 6
Agora para o bloco de cima. Segunda lei de Newton em x:
Corta o :
Substitui os valores:
Resposta
Letra (a):
Letra (b): e
Letra (c): e