Bombeiros estão lançando um jato de água em um prédio em chamas, usando uma mangueira de alta pressão que dispara água a uma velocidade escalar de . Quando sai da mangueira, a água passa a adquirir o movimento de um projétil. Os bombeiros ajustam o ângulo de elevação da mangueira até a água levar para atingir o prédio a de distância. Despreze a resistência do ar e suponha que o final da mangueira está ao nível do solo. a) Ache o ângulo de elevação . b) Ache a velocidade escalar e a aceleração da água no ponto mais alto de sua trajetória. c) A que altura do chão a água atinge o prédio e qual sua velocidade pouco antes de atingir o prédio?
Passo 1
Oi, galerinha! Tudo bom?
Vamos desenhar o que enunciado nos contou!
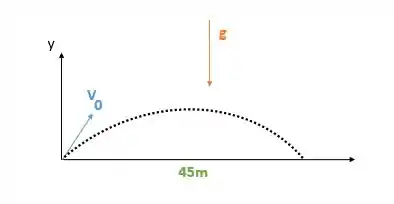
A água percorre horizontalmente () em. E ela está sempre sob a acelaração da gravidade. E vamos tomar como para cima.
A velocidade escalar com que a água sai da torneira pode ser decomposta em duas componentes, uma no eixo e outra no eixo de acordo com o ângulo de elevação :

Assim nós temos que:
Partiu resolver a questão!
Passo 2
- Para encontrarmos o ângulo de elevação vamos partir da equação:
- Vamos decompor o componentes da velocidade, no ponto mais alto, temos que:
- No tempo de: vamos encontrar a posição através da equação:
Como a aceleração no eixo é igual a zero
Vamos substituir a expressão da velocidade no eixo em função da velocidade escalar da água quando sai da mangueira:
Logo:
Substituindo os valores que já conhecemos, como a distância percorrida pela água , a velocidade escalar da água e o tempo :
Encontramos então o ângulo de elevação da mangueira:
Tranquilo até aqui?
Passo 3
A velocidade no eixo não varia, pois a aceleração é sempre igual a . Isso não ocorre no eixo , uma vez que temos a aceleração da gravidade.
Concorda comigo que a velocidade no eixo era positiva antes do ponto máximo da curva, mas depois disso a água começa a cair, então a velocidade se torna negativa considerando o nosso eixo ? Isso ocorre, pois no ponto mais alto da trajetória, a velocidade é igual a:
E então no ponto mais alto da trajetória, a velocidade escalar é:
Como a aceleração do projétil continua sendo a mesma aceleração da gravidade:
E então no ponto mais alto da trajetória, a aceleração escalar é:
Bacana, não é?
Passo 4
Substituindo os valores que já conhecemos:
Está acompanhando?
Passo 3
E então, temos que a velocidade nessas componentes pouco antes de atingir o prédio é de:
Agora a componente em
E então:
E aí! o que achou? Responde Aí!

Resposta
- e
- e