Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.5 - Ex. 54
Calcule o momento de inércia de um aro (um anel fino) de raio e massa em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Passo 1
Oi, galerinha! Tudo bom?
Primeiro vamos entender o que ele pediu. Ele quer o momento de inércia de um aro de raio e massa . Ele mesmo diz que é um anel fino. Mas ele quer esse momento em relaç��o a um eixo que passa pela periferia desse anel. Como assim?
A periferia do anel vai ser qualquer ponto coladinho na borda desse anel. Pode ser, por exemplo, o ponto :
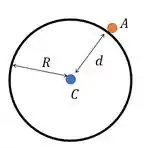
A ideia aqui é que a gente consiga calcular o momento de inércia desse cara em relação a centro de massa dele pela fórmulinha tabelada:
Maaas, como ele pediu para calcular o momento de inércia por um ponto na periferia do arco, o nosso eixo não passa por esse ponto. Por isso, vamos precisar o teorema dos eixos paralelos, ok?
Vamos lá!
Passo 2
Para usar o teorema dos eixos paralelos a gente precisa da distância entre o eixo onde a gente tem o momento (no caso é o centro do aro) e o eixo onde queremos calcular o momento de inércia (no caso é a periferia). A quem chamamos de .
Imagina que nosso eixo passa por . Queremos a distância entre e , que vale . Na figura vemos que é igual ao raio do anel, então
Agora bora aplicar!
Passo 3
A fórmulinha do teorema dos eixos paralelos é
Onde é o momento de inércia em relação ao centro de massa da nossa peça.
Substituindo as quantidades temos:
E aí! o que achou? Responde Aí!
