Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 21.Exercícios - Ex. 42
Uma carga puntiforme é colocada em cada vértice de um quadrado de lado . Todas as cargas possuem módulo . Duas cargas são positivas e duas são negativas (Figura E21.42). Determine a direção e o sentido do campo elétrico resultante no centro do quadrado em função das quatro cargas, bem como o módulo do campo em função de e .
Passo 1
Olá, tudo bem? Vou ajudar você aqui!
O campo elétrico de uma partícula puntiforme é radial, certo? E se ela for positiva é para fora e se ela for negativa, é para dentro. Sendo assim, vou fazer um desenho dos campos elétricos associados às quatro cargas, bem como das suas componentes:
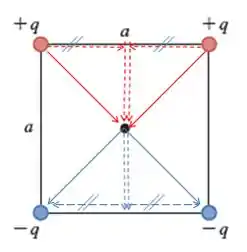
Pelo desenho dá pra ver que só vão sobrar as componentes verticais, então podemos calcular de apenas uma e depois multiplicar por . Como temos uma quadrado, a componente vertical de um dos campos é:
E campo, como temos módulos iguais para as cargas e distâncias iguais (metade da diagonal do quadrado de lado : ), vai ser:
Passo 2
E agora substituindo na componente do campo:
E agora multiplicando por para obtermos o campo resultante:
O campo resultante é na vertical para baixo.