Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 57

Em um certo sistema estelar binário, as duas estrelas têm uma massa igual à do Sol e giram em torno do centro de massa. A distância entre as estrelas é igual à distância entre a Terra e o Sol. Qual é, em anos, o período de revolução das estrelas?

Passo 1

Temos duas estrelas orbitando o centro de massa do sistema formado pelo próprio par. Vamos ilustrar a situação:

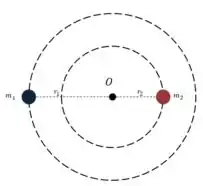
As duas estrelas têm massa igual à do Sol, e a distância entre as duas é igual à distância entre a Terra e o Sol.

Se considerarmos órbitas circulares, podemos dizer que a trajetória circular é sustentada pelas forças gravitacionais, portanto: (vamos discutir a estrela de massa m 1 primeiro)

G m 1 m 2 r 2 = m 1 v 2 r 1

Passo 2

Pela fórmula do centro de massa sabemos que:

m 1 r 1 = m 2 r 2 ⇒ r 2 = m 1 r 1 m 2

Olhando para a figura, temos que:

r = r 1 + r 2

Substituindo o resultado anterior aqui:

r = r 1 + m 1 r 1 m 2 = m 2 r 1 + m 1 r 1 m 2

Ou seja:

r = m 1 + m 2 m 2 r 1

Mas como m 1 = m 2

r = 2 . r 1

Além disso, podemos escrever a velocidade da estrela m 1 :

v = 2   .   π .   r 1 T = π   .   r T

Passo 3

Vamos substituir tudo isso na fórmula anterior, fazendo m 1 = m 2 = m s o l

G . m s o l r 2 = π r / T 2 r / 2

G . m s o l r 2 = 2   π 2 r T 2

Cortando o que for possível e Isolando o período T :

T 2 = 2 π 2 r 3 G . m s o l

Passo 4

Consultando a distância Terra-Sol e a massa do Sol em uma tabela, podemos substituir:

T 2 = 2 . ( 3,14 ) 2 . ( 1,5   ,   10 11 ) 3 6,67   .   10 - 11   .   1,99   .   10 30 = 4,8   .   10 14   s

Logo:

T = 4,84   .   10 14 = 2,2   .   10 7   s

O enunciado pede a resposta em anos terrestres. Uma regra de três simples dá:

T = 2,2   .   10 7 3,156   .   10 7 = 0,71   a n o

Obs.: Porque 1   a n o = 3,156   .   10 7   s

Resposta

T = 0,71   a n o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a)Quando um copo descreve uma órbita circular de raio r em torno da Terra (massa m T ), o período da órbita é igual a T (dado pela Equação (12.12)) e a velocidade orbital é igual a v 9dada pela Equaçã
Mercúrio descreve uma órbita claramente elíptica em torno do Sol. A velocidade de Mercúrio é de 38,8k m / s em seu ponto mais distante, a 6,99 × 10 10k m do Sol. Qual é a distância de Mercúrio ao Sol
Plutão se movimenta em uma órbita claramente elíptica em torno do Sol. A velocidade de Plutão em seu ponto mais próximo, 4,43 × 10 9k m do Sol, é de 6,12k m / s . Qual é a velocidade de Plutão no pont
Os cometas se movimentam em torno do Sol em órbitas muito elípticas. Em seu ponto mais próximo, em 1986, o Cometa Halley estava a 8,79 × 10 7 km do Sol, movendo-se com uma velocidade de 54,6 km/s. Qua
Um planeta está em órbita de uma estrela quando, sem nenhuma razão aparente, a gravidade da estrela desaparece repentinamente. Como ilustra a FIGURA P13.64, o planeta obedece à primeira lei de Newton