Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 25

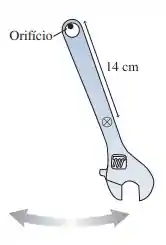
A chave inglesa de 20   c m de comprimento na FIGURA EX14.25 balança em torno de um orifício com período de 0,90   s . Quando a chave está pendurada em uma mola com constante elástica de 360   N / m , ela estica a mola em 3,0   c m . Qual é o momento de inércia da chave em relação ao orifício?

Passo 1

Essa informação do enunciado

Quando a chave está pendurada em uma mola com constante elástica de 360   N / m , ela estica a mola em 3,0   c m .

Serve para você calcular a massa dessa chave, e que será entendida como:

m g = k Δ x

Com k = 360   N / m , Δ x = 3   c m = 3 × 10 - 2   m , então:

m = k Δ x g = 360 ⋅ 3 × 10 - 2 9.81 = 1.1   k g

E por que calcular a massa você me pergunta? Bem, isso é por que essa massa não é puntiforme, ela irá girar em relação ao seu centro de gravidade (há 14   c m do orifício) e isso se caracteriza com um pêndulo físico que tem velocidade angular igual a:

ω = m g l I

Com I sendo a inércia de giro e l o comprimento do orifício até o centro de gravidade.

Passo 2

Então o período desse pêndulo será de:

T = 2 π ω = 2 π   I m g l

Isolando a inércia teremos:

I = T 2 ( m g l ) 4 π 2

Aplicando os valores que o enunciado nos dá teremos:

I = 0.9 2 ( 1.1 ⋅ 9.81 ⋅ 14 × 10 - 2 ) 4 π 2 = 0.031   k g   m 2

Pois essa inércia é a inércia de giro do corpo.

Resposta

0.031   k g   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a amplitude angular θ m das oscilações de um pêndulo simples para a qual a diferença entre o torque restaurador necessário para o movimento harmônico simples e o torque restaurador verdadeir
Suponha que um pêndulo simples é formado por um pequeno peso de 60,0 g pendurado na extremidade de uma corda de massa desprezível. Se o ângulo θ entre a corda e a vertical é dado por θ = 0,0800rad cos
Uma artista de circo, sentada em um trapézio, está balançando com um período de 8,85 s . Quando fica de pé, elevando assim de 35,0 c m o centro de massa do sistema t r a p é z i o + t r a p e z i s t
No laboratório, um aluno de física estuda um pêndulo representando o ângulo θ que o fio faz com a vertical em função do tempo t, obtendo o gráfico mostrado na Figura E13.50. (a) Quais são o período, a
Uma barra de conexão de um motor de automóvel, de 1,80 kg, é suspensa por um eixo horizontal mediante um pivô em forma de cunha, como indicado na Figura E13.55. O centro de gravidade da barra determin