Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.Problemas Adicionais - Ex. 79

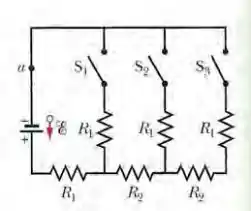
Na Fig. 27-69, R 1 = 20,0 Ω , R 2 = 10,0 Ω e a força eletromotriz da fonte ideal é ε = 120 V . Determine a corrente no ponto a (a) com apenas a chave S 1 fechada; (b) com apenas as chaves S 1 e S 2 fechadas; (c) com as três chaves fechadas.

Passo 1

Neste exercício temos um circuito que pode mudar conforme fechamos as chaves S 1 , S 2 e S 3 e vamos analisar o que acontece quando fechamos as chaves em situações diferentes.

Passo 2

(a) Com a chave S 1 fechada e as chaves S 2 e S 3 abertas,

temos apenas duas resistências R 1 em série logo só temos que somá-las.

ε = 2 R 1 i a

i a = ε 2 R 1 = 120 V 40 , 0 Ω = 3,00 A

R 1 = 20,0 Ω

Passo 3

(b) Com as chaves S 1 e S 2 fechadas e a chave S 3 aberta, temos:

Aqui temos que fazer a resistência equivalente entre R 1 e R 1 + R 2 logo

R e q = R 1 + R 1 R 1 + R 2 2 R 1 + R 2

R 2 = 10,0 Ω

R e q = 20,0 Ω + 20,0 Ω 20,0 Ω + 10,0 Ω 2 × 20,0 Ω + 10 , 0 Ω = 32,00 Ω

logo

i a = ε R e q = 120 V 32,0 Ω = 3,75 A

Passo 4

(c) Com as três chaves fechadas, R e q = R 1 + R 1 R ’ R 1 + R ’ , na qual

R ' = R 2 + R 1 R 1 + R 2 2 R 1 + R 2 = 10,0 Ω + 20,0 Ω × 20,0 Ω + 10,0 Ω 2 × 20,0 Ω + 10,0 Ω = 22,00 Ω

e temos:

R e q = R 1 + R 1 R ’ R 1 + R ’ = 20,0 Ω + 20,0 Ω × 22 , 00 Ω 2 × 20,0 Ω + 10,0 Ω = 30,50 Ω

i a = ε R e q = 120 V 30,5 Ω = 3,94 A

Resposta

(a) i a = 3,00 A

(b) i a = 3,75 A

(c) i a = 3,94 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

65- ( a ) Calcule o potencial do ponto a em relação ao ponto b na Figura 26.69 . ( b ) Sabendo que os pontos a e b são conectados por um fio de resistência desprezível, calcule a corrente que passa na
66- Considere o circuito indicado na Figura 26.70 : ( a ) Qual deve ser a fem ϵ da bateria para que uma corrente de 2.0A passe pela bateria de 5.0V , conforme indicado? A polaridade da bateria está co
69- No circuito indicado na Figura 26.73 , a corrente na bateria de 20.0V é igual a 5.0A no sentido indicado, e a voltagem através do resistor de 8.0Ω é de 16.0V , com a extremidade inferior do resist
Suponha que um resistor com resistência R esteja sobre cada aresta de um cubo (um total de 12 resistores) e que os resistores sejam conectados a través dos vértices do cubo. Calcule a resistência equi
Malha infinita. A rede com resistores R 1 e R 2 indicados na Figura 26.83 se estende até o infinito pelo lado direito. Prove que a resistência total R T dessa rede infinita é dada por:(Sugestão: uma v