Uma viga irregular de está pendurada horizontalmente por suas extremidades em um teto por dois fios verticais (A e B), cada um com de comprimento e pesando . O centro de gravidade dessa viga está a um terço da viga a partir da extremidade em que o fio A está amarrado. Se você puxar ambas as cordas ao mesmo tempo, qual será o intervalo de tempo entre a chegada dos dois pulsos ao teto? Que pulso chegará primeiro?
Passo 1
Olá tudo bem? Essa questão parece complicada, mas vou facilitar para você! Vamos começar?
Temos uma viga pesando pendurada por dois fios. Os fios tem de comprimento e pesam cada um . A viga não é homogênea e seu centro de gravidade (onde podemos considerar que o peso está todo concentrado) está a um terço de onde o fio A está amarrado. Então com todas essas informações vamos fazer um esquema da situação:
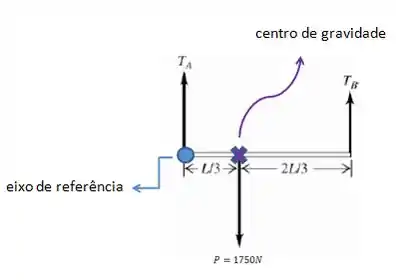
Se o centro de gravidade está a do fio A, então o fio B está a do centro de gravidade. Para determinar o tempo que cada pulso leva para percorrer a corda, precisamos da velocidade de propagação. Com a velocidade (que se relaciona com a densidade linear), e sabendo que ela é constante, podemos determinar o tempo em cada pedaço da corda , certo? Essa é a ideia aqui! Mas, vamos por partes, ok?
Passo 2
A densidade linear de cada corda é igual e vale:
Passo 3
Para achar a velocidade de propagação será preciso determinar as tensões e dos fios. Aqui vou usar um conceito já familiar: o torque! A barra está em equilíbrio, portanto ela não está girando. Então temos que a soma de todos os torques é zero! Supondo que o eixo de rotação é o eixo de referência indicado na figura do passo 1, temos que levar em conta dois torques: proveniente da tensão e do peso :
E sabemos que a barra está totalmente suspensa pelas tensões, então a soma das tensões deve ser igual ao seu peso:
Passo 4
Beleza! Agora que determinamos as tensões, podemos determinar as velocidades de propagação em cada um dos fios. Lembrando que , e que as densidades são iguais, as velocidades serão:
Passo 5
Agora podemos calcular o tempo que cada pulso leva! Lembrando que o comprimento de cada fio é , os tempos são:
Passo 6
O intervalo de tempo entre os pulsos será a diferença entre os tempos que acabamos de determinar:
E o pulso que vai chegar mais rápido é o pulso no fio A, pois sua tensão é maior =)