Uma corda fina, esticada, presa nas duas extremidades e oscilando em seu terceiro harmônico possui a forma descrita pela equação , onde a origem está na extremidade esquerda da corda, o eixo está na corda e o eixo é perpendicular à corda.

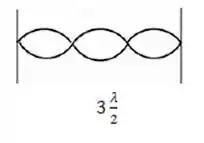
1. Desenhe um diagrama que mostra a configuração da onda estacionária.
2. Calcule a amplitude das duas ondas progressivas que compõem essa onda estacionária.
3. Qual é o comprimento da corda?
4. Calcule o comprimento de onda, a frequência, o período e a velocidade máxima de um ponto da corda.
5. Calcule a velocidade transversal máxima de um ponto da corda.
6. Qual seria a equação para essa corda se ela estivesse vibrando em seu oitavo harmônico?

Letra b)

A equação da onda é:

E em comparação com a equação geral da onda temos que a amplitude da onda estacionária é . Assim a amplitude da onda é a metade da amplitude da onda estacionária:

Letra c)

Como vimos no passo , temos comprimentos de onda no terceiro harmônico. Como a distância entre as extremidades vale :

E o comprimento de onda está relacionado com o número de onda :

E em comparação com a equação geral, temos que , assim conseguimos calcular o valor de :

Letra d)

Como sabemos que e o tamanho da corda é , ficou tranquilo encontrar o comprimento de onda:

A frequência pode ser encontrada a partir de :

O período é o inverso da frequência:

E a velocidade é o produto da frequência pelo comprimento de onda:

Letra e)

A velocidade transversal está relacionada com a amplitude e com a frequência angular:

Letra f)

Para determinar a equação para o oitavo harmônico precisamos determinar , comprimento de onda , e correspondentes.

Como temos a frequência do terceiro harmônico, podemos calcular a frequência fundamental:

E assim calcular a frequência :

E temos :

E o comprimento de onda:

E agora o número de onda:

Agora podemos construir a equação para o oitavo harmônico: