Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.7 - Ex. 47
Um corpo de está se movendo no sentido positivo de um eixo com uma velocidade de quando, devido a uma explosão interna, se quebra em três pedaços. Um dos pedaços, com uma massa de , se afasta do ponto da explosão com uma velocidade de no sentido positivo do eixo . Um segundo pedaço, com uma massa de , se move no sentido negativo do eixo x com uma velocidade de .
Em termos dos vetores unitários, qual é a velocidade da terceira parte?
Qual é a energia liberada na explosão? Ignore os efeitos da força gravitacional.
Passo 1
Desenhando a situação retratada no enunciado antes e depois da explosão nós temos:
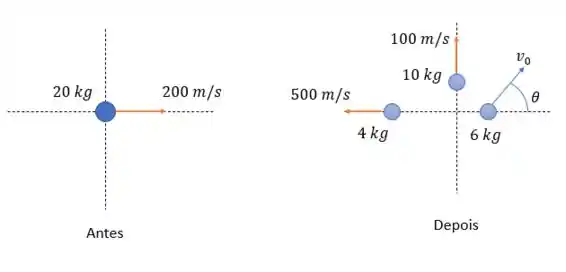
Como a massa não é destruída então a soma das três massas após a explosão tem que ser a massa total do corpo antes da explosão e será de .
Fazendo agora a conservação do momento linear nós temos:
Então:
Igualando os termos que contém nós temos:
E igualando os termos com :
Passo 2
Dividindo a segunda equação pela primeira teremos:
Então:
Só que como queremos a velocidade em termos dos vetores unitários então:
Não precisava ter achado o e mas eu achei melhor que você entendesse essa forma que eu fiz que é bem útil.
Passo 3
Agora para a letra , a energia antes da explosão é marcada somente pela energia cinética e vale:
E a energia cinética total dos corpos depois da explosão será dada por:
Acabou que foi útil encontrar .
Então temos um modelo de energia igual a:
Onde é a energia cinética inicial e a energia cinética final e sua diferença será causado por que é a energia da explosão, que será: