Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 51

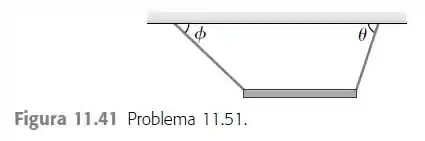
Uma viga de massa M e comprimento L é horizontalmente sustentada nas suas extremidades por dois cabos que formam ângulos θ e ϕ com o teto horizontal (Figura 11.41). a) Mostre que,

se a viga for homogênea, esses dois ângulos devem ser iguais e as tensões nos cabos também devem ser iguais. b) Suponha que o centro de gravidade está a 3L/4 da extremidade esquerda da viga. Mostre que os ângulos não são completamente independentes, mas que devem obedecer à equação tan ⁡ θ   3 tan ⁡ ϕ .

Passo 1

Precisamos aplicar as condições de equilíbrio à viga.

Primeiro vamos esboçar um diagrama de corpo livre para a viga:

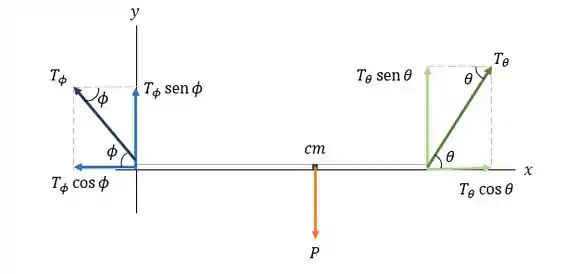
Seja T ϕ e T θ a tensão nos dois cabos.

Cada tensão foi substituída por seus componentes horizontais e verticais.

Passo 2

  1. O centro de gravidade do feixe está a uma distância L / 2 de cada extremidade e ∑ τ = 0   om o eixo no centro de gravidade do feixe nos dá que:

    2. - T ϕ sen ⁡ ϕ L 2 + T θ sen ⁡ θ L 2 = 0

    Isso implica que:

    T θ sen ⁡ θ = T ϕ sen ⁡ ϕ

    Passo 3

    E aplicando a segunda condição, temos que:

    ∑ F x = 0

    T θ sen ⁡ θ = T ϕ sen ⁡ ϕ

    Dividindo a primeira equação pela segunda, ficamos com:

    tan ⁡ ϕ = tan ⁡ θ

    E assim, temos que:

    ϕ = θ

    então as equações também nos dizem que:

    T ϕ = T θ  

    Passo 4

  2. O centro de gravidade do feixe fica a uma distância de 3 L / 4 da extremidade esquerda, portanto, a uma distância de L / 4 da direita fim.

Aplicando ∑ τ = 0   com o eixo no centro de gravidade do feixe dá:

- T ϕ sen ⁡ ϕ 3 L 2 + T θ sen ⁡ θ L 2 = 0

E

3 T ϕ sen ⁡ ϕ = T θ sen ⁡ θ

Passo 3

E aplicando a segunda condição, temos que:

∑ F x = 0

T ϕ cos ⁡ ϕ = T θ cos ⁡ θ

Dividir a primeira equação pela segunda , temos que:

3 tan ⁡ ϕ = tan ⁡ θ

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pessoas transportam uma prancha de madeira uniforme com 3,0 m de comprimento e peso de 160 N. Se uma das pessoas aplica em uma extremidade uma força de baixo para cimade 60 N, em qual ponto a out
Uma escada uniforme de 5,0m de comprimento repousa contra uma parede vertical sem atrito e sua extremidade inferior está situada a 3,0m da parede. A escada pesa 160N . O coeficiente de atrito estático
Determine a tensão T em cada cabo e o módulo, a direção e o sentido da força exercida sobre a viga pelo pivô em cada um dos arranjos indicados na Figura 11.26. Em cada caso, seja p o peso da caixa sus
Em um jardim zoológico, uma barra uniforme de 3,0 m de comprimento e 240 N é mantida em posição horizontal por meio de duas cordas amarradas em suas extremidades (Figura 11.30). Acorda da esquerda faz
Uma porta de 1,0 m de largura e 2,0 m de altura pesa 280 N e é suportada por duas dobradiças, uma situada a 0,50 m a partir do topo e a outra a 0,50 m a partir do ponto inferior. Cada dobradiça suport