Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 49

A extremidade da barra da Figura repousa sobre uma superfície horizontal sem atrito, e a extremidade está articulada. Uma força horizontal de módulo igual a é aplicada à extremidade . Despreze o peso da barra. Determine os componentes vertical e horizontal da força exercida pela barra sobre a articulação no ponto .

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente calcular os componentes vertical e horizontal da força exercida pela barra sobre a articulação no ponto .

Observe que a componente horizontal da força exercida na barra pela articulação em deve ser equilibrada pela força pela força aplicada . Então, ela vai ter a mesma magnitude de e sentido para esquerda. E a componente vertical dessa força na articulação, vai equilibrar a força normal exercida na barra, observe o diagrama de corpo livre (DCL) do sistema:

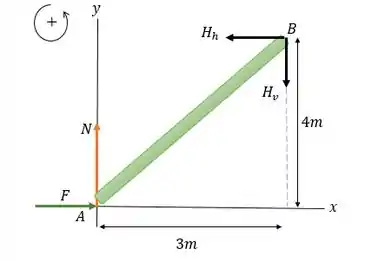
Não há força de atrito nesta superfície da barra. e são os componentes da força exercida na barra pela dobradiça. Dessa forma, os componentes da força na barra são iguais em magnitude e opostos em direção. Com base nisso, vamos construir as nossas equações de equilíbrio e obter os valores de e .

Vamos lá!

Passo 2

Então, aplicando as condições de equilíbrio, temos que e . Fazendo o somatório das forças horizontais presentes no nosso DCL, temos:

Como vimos no passo anterior tem a mesma magnitude de .

Agora somando as forças verticais, vamos ter:

Então, isolando a componente na equação, obtemos:

Mas não conhecemos o valor de , então vamos usar a segunda condição de equilíbrio para calcula-la.

Passo 3

Para que haja equilíbrio, temos que o somatório dos torque tem que ser zero, ou seja:

Então, calculando os torque exercidos no ponto da nossa barra, teremos:

E isolando na equação:

Como , temos:

E então, pela equação do passo , obtemos:

Logo, a força da barra na dobradiça tem uma componente horizontal de , para a direita, e uma componente vertical de , para cima.

Valeu, galera! Até a próxima! 😉

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o pé de um corredor atinge o chão, a força de cisalhamento atuando sobre um solado de 8,0m m de espessura é como a mostrada na Figura 12-46. Se a força de 25N é distribuída sobre uma área de 15

Um cilindro, de massa M e raio R , rola até um degrau de altura h , como mostrado na figura. Quando uma força horizontal de magnitude F é aplicada no topo do cilindro, este permanece em repouso. (a) D

A Figura 12-62 mostra uma prancha homogênea, de 20 cm de comprimento, sobre um cilindro de 4,00 cm de raio. A massa da prancha é 5,0 kg e a do cilindro é 8,0 kg. O coeficiente de atrito estático entre

Um cubo maciço de aresta a, equilibrado sobre um cilindro de diâmetro d, está em equilíbrio instável se d ≪ a (Figura 12-64), e está em equilíbrio estável se d ≫ a . O cubo não escorrega sobre o cilin

Duas esferas maciças e polidas (sem atrito), de raio r, são colocadas dentro de um cilindro de raio R, como na Figura 12-63. A massa de cada esfera é m. Determine a força exercida pela base do cilindr