Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 43
O despachante de bagagem de um aeroporto deixa cair sua sacola de viagem, de , sobre a esteira rolante que está passando abaixo a . Os materiais são tais que e. Ao longo de que distância sua sacola irá escorregar sobre a superfície da esteira até passar a deslocar-se junto dela, sem escorregar?
Passo 1
Vamos analisar primeiro o que está acontecendo aqui:
A esteira já está em movimento, e quando a sacola de viagem cai sobre a esteira ela ganha uma aceleração no sentido do movimento da esteira, na direção positiva. Para que a sacola ganha essa aceleração, ela precisa estar sob a ação de uma força na mesma direção e sentido e essa força será a força de atrito cinético da esteira com a sacola.
Essa força age até que a sacola atinja a mesma velocidade constante da esteira e entre em equilíbrio.
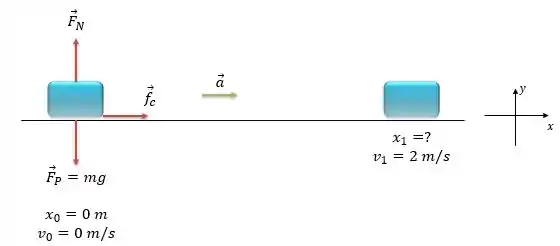
Passo 2
A sacola não se movimenta na direção , então:
A massa é fornecida na questão e a aceleração da gravidade é conhecida:
Passo 3
O módulo da força de atrito pode ser escrito como:
Tendo a força normal já calculada e sabendo que:
A força de atrito vale:
Passo 4
Agora, podemos calcular a aceleração que a sacola adquire na direção , através da segunda lei de Newton:
Passo 5
Tendo a aceleração, utilizamos a equação de Torricelli, para achar a distância percorrida, , pela sacola até atingir a velocidade
Então: