Sam, com de massa, dispara com seus esquis a jato descendo uma rampa de verticais de altura e de inclinação. Os esquis desenvolvem um empuxo de . Na base da rampa, Sam atinge uma velocidade de . Qual é o coeficiente de atrito dos esquis com a neve?
Passo 1
Vamos começar desenhando a situação, beleza?
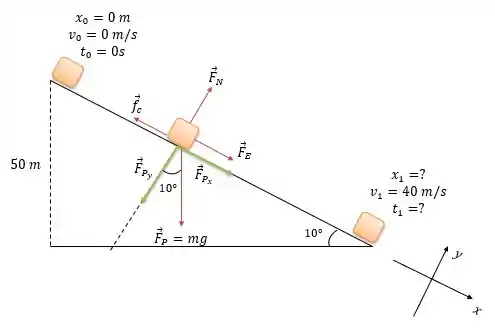
Aí está o esquema da situação e as forças que atuam sobre o menino.
De acordo com o sistema de coordenadas adotado, podemos decompor a força peso em uma componente e outra componente :
Sempre lembrando: COlado – COsseno; SEparado – SEno
Passo 2
Vamos calcular o comprimento do plano inclinado utilizando o ângulo que ele forma com a horizontal e a sua altura:
Podemos escrever o comprimento em função da posição final e inicial do menino que esquia sobre o plano:
Logo:
Tendo que:
Temos:
Passo 3
Sabendo a diferença podemos calcular a aceleração do menino, utilizando a equação de Torricelli:
e foram fornecidos na questão e a diferença entre a posição final e inicial nós calculamos. Substituindo os valores:
Passo 4
Agora, vamos aplicar a segunda lei de Newton para a direção :
A massa e a intensidade da força de empuxo foram fornecidas na questão, a aceleração da gravidade é um valor conhecido e a aceleração nós calculamos, assim conseguimos calcular a intensidade da força de atrito:
Note que a força de atrito deu negativa porque ela está no sentido negativo do eixo , beleza?
Passo 5
O módulo da força de atrito pode ser escrito como:
Para sabermos quem é vamos dizer que o somatório de forças na direção é zero, porque não há movimento nessa direção:
Temos que:
Então:
Passo 6
Conhecendo a força normal e a força de atrito conseguimos calcular o coeficiente de atrito:
Fechamos =)