Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 27
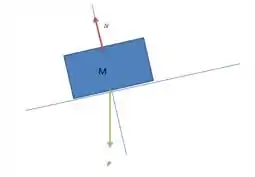
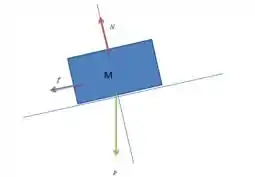
Diagramas do corpo livre. As duas etapas iniciais para aplicar a segunda lei de Newton para resolver um problema são isolar um corpo para análise e, a seguir, fazer um diagrama do corpo livre para indicar as forças que atuam sobre o corpo escolhido.
Desenhe diagramas do corpo livre para as seguintes situações:
a) um bloco de massa deslizando para baixo ao longo de um plano inclinado, sem atrito e formando um ângulo com a horizontal;
b) um bloco de massa deslizando para cima ao longo de um plano inclinado, sem atrito e formando um ângulo com a horizontal;
c) um bloco de massa deslizando para cima ao longo de um plano inclinado com atrito cinético, formando um ângulo com a horizontal.
Passo 1
No primeiro caso temos apenas a força normal (perpendicular a superfície de contato para cima) e a força peso (perpendicular ao chão para baixo) agindo sobre o bloco.
O diagrama de forças para esse caso pode ser representado assim:
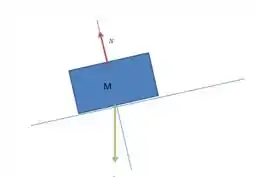
Passo 2
No segundo caso temos que agora o bloco está deslizando para cima. Entretanto em questão de força não há mudanças em relação ao primeiro caso! As forças que agem sobre ele são as mesmas e o diagrama de forças fica idêntico:
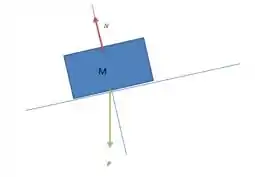
Passo 3
No terceiro caso temos uma força adicional: a força de atrito ! Essa é SEMPRE contrária ao movimento! Então se o bloco está se deslocando para cima, a força aponta para baixo na direção de movimento do plano. O diagrama fica assim ó:
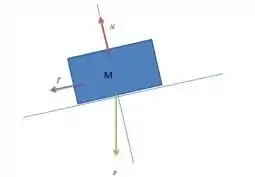
Resposta
