Distancia temporal entre dois eventos. Os eventos e ocorrem nas seguintes coordenadas espaçotemporais nos referenciais da Fig. 37-25: no referencia , e ; no referencial , e . No referencial , e . (a) Escreva uma expressão para em termos do parâmetro de velocidade e dos dados do problema. Faça um gráfico de em função de (b) para e (c) para . (d) Para que valor de o valor de é nulo?
Passo 1
Para resolvermos esse problema, vamos utilizar a Eq. 1’ da tabela 37-2, onde relacionamos a posição do evento no referencial com o tempo e a posição no referencial em função do fator . Vamos também plotar os gráficos após termos a equação de em função de e encontrar os valores para qual a função se anula.
Passo 2
- Vamos começar utilizando a equação mencionada no passo 1. Ela é da seguinte forma
- Para plotarmos o gráfico, vamos analisar a equação. Temos que para valores muito pequenos de , será aproximadamente 1. Dessa forma, temos que para o primeiro intervalo onde a equação ficará como de primeiro grau, da forma
- Para esse novo intervalo, temos que a equação será do tipo
- Para encontrarmos o valor de para qual é nulo, temos que igualar a equação a zero. Assim, ficamos com
Substituindo os valores dados no problema, temos que , e
. Assim, a equação fica
Com variando com da seguinte forma
Passo 3
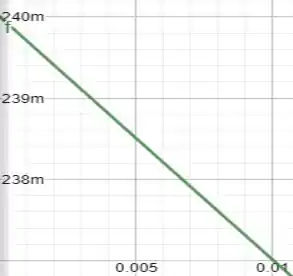
Passo 4
E para o intervalo dado, temos que a equação se comportará da seguinte forma
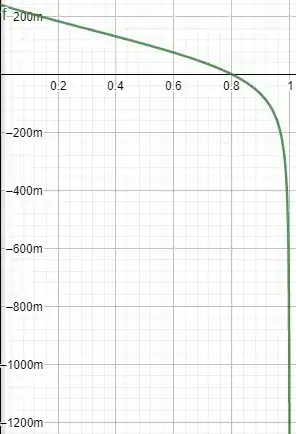
Passo 5
Temos que a única maneira dessa equação respeitar a igualdade é se
Resposta
a)
d)