54. Diz-se que Galileu descobriu um princípio básico do pêndulo – o de que o período independe da amplitude – usando sua pulsação para medir o período das oscilações dos candelabros de uma catedral, postos em movimento pela brisa. Suponha que uma oscilação de um candelabro leve .

a. Qual é o comprimento da corrente do candelabro?

b. Que valor de velocidade máxima atinge o candelabro se sua posição angular máxima, em relação à vertical, é de ?

b) Nessa letra, estamos nos deparando com talvez, a questão mais repetida da história dos livros de física, a velha questão do pêndulo.

Esssa questão cai em Termologia, cai em Mecânica, cai em Ondulatória. Só faltava cair em Óptica! Aí é o fim da picada!

Sem perder tempo! Todo mundo aqui já sabe o que tem que fazer, né!?

É só usar a conservação da energia! Mas como a gente é cuidadoso, antes, vamos fazer um esboço do problema....

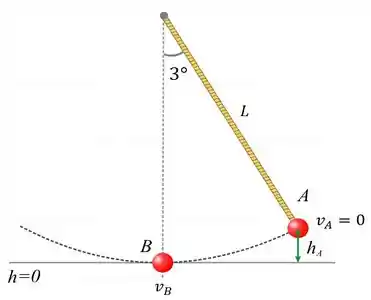
É claro que isso é uma bola! Mas pelo bem da humanidade, bora fingir que é um candelabro, né!?

E em seguida, vamos usar a conservação da energia. No caso, igualaremos as energia em e em :

Quando o candelabro passa pelo ponto , a energia potencial dele é nula e ele está em sua velocidade máxima. Já quando ele atinge , a velocidade se anula e o único tipo de energia presente, é a potencial gravitacional. Desse modo...

Como queremos a velocidade máxima , a incógnita aqui, é a altura .

Bem! Não é mais! Pela figura, podemos ver que é dada por...

O que nos faz ficar com...

E como da letra anterior, sabemos o valor de :

Descobrimos nossa resposta e nos vemos na próxima!

Tcccccchauuu!