Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 58
58. Uma das extremidades de uma haste de de comprimento é fixada por um pino. Uma bola de argila de é presa à outra extremidade. Qual é o período se o bastão e a argila balançam como um pêndulo?
Passo 1
Se liga só! Pra essa questão não ficar “mamão com açúcar”, bora considerar que nosso bastão tem uma massa de . De acordo com a figura abaixo...
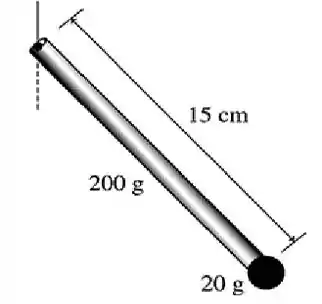
Desse modo, o momento de inércia total desse nosso sistema, vai ser dado pela soma do momento de inércia da haste com o momento de inércia da bola em relação ao eixo de rotação. Logo, pelo teorema dos eixos perpendiculares...
Substituindos os valores numéricos de cada variável....
Passo 2
Em seguida, bora calcular o valor do centro de massa desse sistema. Considerando, é claro, que ele esteja localizado na direção em que está a haste.
A fórmula do centro de massa é dada por...
Onde representa o somatório do produto da massa pela posição de seu centro de massa e representa o somatório das massas.
Desse modo, levando para a situação do nosso problema, o centro de massa vai ser...
Passo 3
E obtida a posição do centro de massa, vamos usar a fórmula abaixo para a frequência angular em um pêndulo...
Onde é a distância entre o eixo de rotação e o eixo do centro de massa, ou seja o nosso . Substituindo assim, os valores das outras variáveis...
Como o período é o inverso da frequência...
Pronto! Esse é o período do nosso bastão, que se comporta como um pêndulo!