Dois astros iguais de massa , , são acelerados um em direção ao outro, a partir do repouso, pela força gravitacional mútua. A distância inicial entre os centros dos dois astros é . Suponha que um observador se encontra em um referencial inercial estacionário em relação ao centro de massa deste sistema de dois corpos. Use a lei de conservação da energia mecânica para determinar as seguintes grandezas quando a distância entre os centros é : (a) a energia cinética total do sistema, (b) a energia cinética de cada astro, (c) a velocidade escalar de cada astro em relação ao observador e (d) a velocidade do astro em relação ao astro .
Em seguida, suponha que o referencial do observador está ligado ao astro (ou seja, o observador se encontra no astro ). Nesse caso, o observador vê o corpo acelerar em sua direção a partir do repouso. Neste referencial, use novamente a relação para determinar as seguintes grandezas quando a distância entre os centros é : (e) a energia cinética do astro e (f) a velocidade escalar do astro em relação ao astro . (g) Por que as respostas dos itens (d) e (f) são diferentes? Qual das duas respostas está correta?
Passo 1
Vamos começar desenhando a situação:
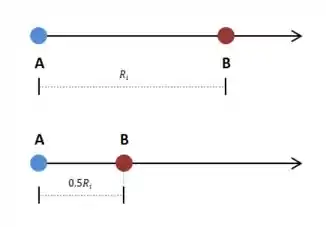
Ao longo do exercício, vamos aplicar a lei de conservação de energia entre esses dois estados:
Passo 2
A letra (a) quer a energia cinética total do sistema. Como os dois astros partem do repouso, , ou seja:
E substituindo as fórmulas ficamos com:
E essa é a resposta da letra (a).
Passo 3
Na letra (b), queremos a energia cinética de cada astro.
Olha, os dois astros têm a mesma massa, e estamos no referencial do centro de massa, que é “neutro”, então não tem nenhum motivo pra um astro se comportar diferente do outro.
Ou seja, podemos dizer que a energia cinética de cada astro é a metade da energia cinética total:
E essa é a resposta da letra (b).
Passo 4
Para a letra (c), queremos a velocidade escalar de cada astro quando a distância entre os dois é .
Acabamos de calcular a energia cinética de cada corpo nesse momento, para achar a velocidade que corresponde a isso:
Passo 5
A letra (d) quer a velocidade do astro em relação ao astro nesse momento.
Já falamos que os dois astros se comportam de forma simétrica, como se um fosse um espelho do outro. Nesses casos, assim como em uma colisão frontal, a velocidade escalar de um em relação ao outro é simplesmente o dobro da velocidade escalar em relação ao centro de massa:
E essa é a resposta da letra (d).
Passo 6
A partir da letra (e), vamos basicamente refazer os outros itens colocando o referencial no astro .
Quando colocamos o referencial em um objeto, sempre consideramos tudo como se esse objeto estivesse parado, ou seja, vamos considerar tudo como se o astro estivesse parado, e o resto do mundo se movendo.
Como a energia cinética total do sistema deve ser a mesma, e a do astro A deve ser nula, toda a energia do sistema vai estar concentrada no astro :
E essa é a resposta da letra (e).
Passo 7
E na letra (f), queremos a velocidade escalar do astro em relação ao astro nesse mesmo momento.
Basta calcular a velocidade associada à energia cinética que acabamos de calcular:
Passo 8
Finalmente, a letra (g) pede para respondermos qual das duas respostas (a da letra (d) ou da letra (f)) está correta.
As duas questões pediam para calcularmos a velocidade escalar do astro em relação ao astro , mas partiam de cálculos de energia em referenciais diferentes.
A letra (d) dizia:
E a letra (f) dizia:
Mas existe uma diferença fundamental entre os referenciais: como o astro sofre aceleração, o referencial que colocamos sobre ele é não inercial, enquanto o referencial do centro de massa é inercial.
As fórmulas que usamos para energia só podem ser aplicadas corretamente em referenciais inerciais. Portanto, a resposta da letra (f) está errada.
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
(g) A resposta da letra (f) está incorreta.