Duas estrelas de nêutrons estão separadas por uma distância de . Ambas têm uma massa de e um raio de . As estrelas se encontram inicialmente em repouso. Com que velocidade estarão se movendo, em relação a este referencial de repouso, (a) quando a distância for metade do valor inicial e (b) quando estiverem na iminência de colidir.
Passo 1
(a) A situação inicial é a seguinte: duas estrelas de nêutrons separadas por uma distância , com massas e raios .
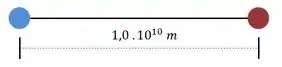
Estamos falando da energia de um sistema que está mudando com o tempo: isso sugere fortemente a aplicação da lei da conservação de energia. E é isso o que faremos aqui:
Passo 2
Vamos aplicar essa lei para o sistema inteiro.
A energia cinética inicial é nula, pois as estrelas parte do repouso, então . Como queremos encontrar a velocidade ao final de certo deslocamento, queremos obter .
Para a energia potencial inicial, vamos usar a fórmula para a energia potencial gravitacional entre dois corpos:
Uma vez que ambas as massas são iguais a e a distância entre os centros das estrelas é .
Para a energia potencial final, podemos usar o fato de que, no nosso estado final, a distância entre os corpos é metade da distância inicial. Então:
Substituindo tudo isso na lei de conservação de energia:
Isolando o que queremos encontrar:
Passo 3
Agora é só obter a velocidade a partir da energia cinética final. É importante lembrar que estamos aplicando a lei de conservação sobre o sistema inteiro, então temos que somar as energias cinéticas das duas estrelas:
Cortando e isolando a velocidade , obtemos:
Ajustando para dois algarismos significativos (conforme o enunciado):
Pronto!
Passo 4
Para o item (b) a lógica será muito parecida, mas como agora estamos na iminência da colisão, teremos:

Portanto a única mudança em relação à conta que fizemos no item anterior vai ser na :
Aplicando a conservação de energia:
Cortando uma vez a massa e isolando a velocidade :
A fração é muito pequena, então podemos simplesmente descarta-la na subtração:
Ajustando para dois algarismos significativos:
Pronto!
Resposta
(a)
(b)