Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 54
Dois carros viajam ao longo de uma estrada reta. O carro A mantém uma rapidez constante de 80 km/h e o carro B mantém uma rapidez constante de 110 km/h. Em t=0, o carro B está 45 km atrás do carro A. (a) Quanto mais viajará o carro A até ser ultrapassado pelo carro B? (b) Quanto à frente do carro A estará o carro B 30 s após tê-lo ultrapassado?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado nos diz que o carro A está 45 km a frente do carro B no momento inicial. Nos é pedido então o tempo até o carro A ser ultrapassado, já que B está mais rápido (com velocidade maior).
A ultrapassagem ocorre quando as coordenadas de posição forem as mesmas:
Como os nossos carros estão à velocidade constante, a posição deles em relação ao tempo pode ser descrita pela equação
Onde é a posição em e é a velocidade do carro. Escrevendo essa expressão para o carro e para o carro
Vamos montar essas expressões com os dados que ele deu e achar o que satisfaz . Bora!
Passo 2
Como ele diz que em , o está atrás do , vamos colocar a nossa origem do referencial em , e dizer que e ,
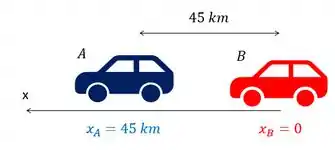
e o enunciado diz que que e , nossas expressões ficam
E para
Lembrando que queremos o onde essas duas posições são iguais, então
Passo 3
b) Agora, vamos analisar a distância entre os carros após 30 s da ultrapassagem.
A distância entre eles é dada pela módulo da diferença entre suas posições:
Mas lembra que
Substituindo essas posições na expressão
Passo 4
Mas quem é agora? Cara, ele é o tempo de depois da ultrapassagem. Vimos que a ultrapassagem foi em , então o tempo que queremos aqui é
Como as velocidades estão em km/h e o tempo em segundos, iremos transformar o tempo para horas. Vamos dividi-lo por que é a quantidade de segundos dentro de uma hora
Logo:
Substituindo isso na nossa expressão
Mas lembra que a distância é o módulo dessa difereça, então