Exercícios de Poder de Resolução e Critério de Rayleigh - Lista de Exercícios Resolvida
Questão 1
A pupila do olho de uma pessoa tem um diâmetro de . De acordo com o critério de Rayleigh, qual deve ser a distância entre dois pequenos objetos para que estejam no limite da resolução quando se encontram a de distância do olho?
Suponha que o comprimento de onda da luz é .
Ver solução completaQuestão 2
Um astronauta a bordo de um ônibus espacial afirma que pode resolver com dificuldade dois pontos sobre a superfície da Terra, abaixo. Calcule:
- A separação angular dos pontos
- A separação linear dos pontos
Suponha condições ideais. Tome como o comprimento de onda da luz e como o diâmetro da pupila do astronauta.
Ver solução completaQuestão 3
Os dois faróis de um automóvel que se aproxima de um observador estão separados por uma distância de . Qual é:
- A separação angula mínima?
- A distância mínima para que o olho do observador seja capaz de resolvê-los?
Suponha que o diâmetro da pupila do observador é e use um comprimento de onda da luz de para a luz dos faróis.
Suponha também que a resolução é limitada apenas pelos efeitos da difração e, portanto, que o critério de Rayleigh pode ser aplicado.
Ver solução completaQuestão 4
Os dois faróis de um automóvel distam . Ele se aproxima de um observador cuja pupila tem diâmetro de . A luz emitida pelos faróis tem comprimento de onde de . Admita o Critério de Rayleigh nessas circunstâncias.
Calcule a distância mínima entre o automóvel e o observador para que esses faróis possam ser distinguodos como objetos separados.
Ver solução completaQuestão 5
Um satélite espião está em órbita circular a uma altitude de 650 km. Calcule o diâmetro da lente da câmera do satélite para que as fotografias tiradas com luz de comprimento de onda de 480 nm tenham uma resolução limite de 25 cm.
Ver solução completaQuestão 6
Qual é a distância mínima que deve separar dois objetos na Lua para serem resolvidos pelo telescópio espacial Hubble que tem um espelho de de diâmetro?
Considere a distância entre o Hubble e a Lua e o comprimento de onda da luz (luz violeta).
Ver solução completaQuestão 7
Considere um quadro pontilhista, feito com pontos circulares de tinta, separados por uma distância média de (o quadro não foi feito com tinta espalhada continuamente). Se olharmos de muito perto distinguiremos os pontos, mas se olharmos de longe, teremos a impressão de que o quadro foi pintado de forma contínua.
Se considerarmos que o comprimento médio da luz visível é de e que a pupila humana tem um diâmetro de , a distância mínima entre o quadro e nossos olhos, que nos permite distinguir os pontos será de aproximadamente igual a:
Nenhuma das anteriores
Ver solução completaQuestão 8
(II) Duas fontes e não coerentes emitem luz no mesmo comprimento de onda . A distância entre as fontes é e ambas se situam à mesma distância de um anteparo com uma fenda de largura . A imagem das fontes é projetada sobre uma tela, conforme a figura. Deduza a dependência entre , , e para que as imagens na tela estejam resolvidas.
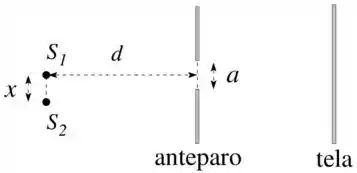
Questão 9
Dois objetos separados por uma distância D = 5,0 cm emitem radiação eletromagnética com comprimento de onda de 15 nm. Esses objetos distam L de um dispositivo eletromagnético dotado de uma “lente” com diâmetro 4,0 mm. Use o critério de Rayleigh para obter a distância máxima entre o dispositivo e os objetos, de modo que esses objetos possam ser distinguidos um do outro.
Ver solução completaQuestão 10
Se você consegue ler a última linha do quadro no exame de vista de seu oculista, o poder de resolução do seu olho corresponde a cerca de um minuto de arco, equivalente a do grau.
Caso esse limite de resolução seja oriundo de efeitos de difração, a que diâmetro efetivo do sistema ótico do seu olho essa resolução corresponde?
Use o critério de Rayleigh e suponha .
Ver solução completaQuestão 11
Uma fenda estreita é iluminada por uma fonte monocromática puntiforme a uma distância da fenda, produzindo uma figura de difração sobre uma tela distante de da fenda.
A distância entre os mínimos adjacentes ao máximo principal nessa figura é de .
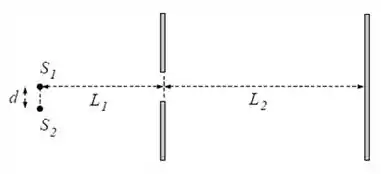
- Se a largura da fenda for duplicada, qual será a nova distância entre os mínimos adjacentes ao máximo principal na figura de difração? Justifique sua resposta.
- Nas condições do enunciado, uma segunda fonte puntiforme , idêntica mas não coerente com a primeira fonte, é colocada a uma distância da fonte original, paralelamente à direção da largura da fenda.
Qual é o menor valor de para que ainda seja possível identificar pela figura de difração na tela a presença de duas fontes distintas?
Ver solução completaQuestão 12
Luz de comprimento de onda de de uma fonte pontual distante incide normalmente sobre um anteparo com uma fenda de largura . O padrão de difração é observado numa tela a uma distância do anteparo.
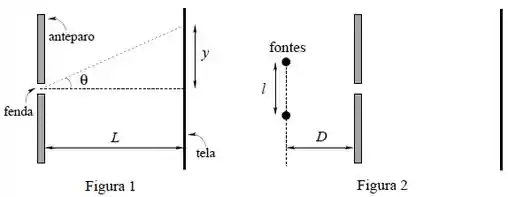
- Calcule a posição angular do primeiro e do segundo mínimos de difração com (use a aproximação ).
- Calcule a distância do primeiro máximo lateral de difração em relação ao centro da figura de difração (veja a figura 1). Use a aproximação de que um máximo lateral está situado à meia distância dos mínimos adjacentes.
- Considere agora duas fontes pontuais idênticas, não coerentes, emitindo luz desse mesmo comprimento de onda (), situadas à mesma distância da fenda e separadas por , conforme a figura 2. Determine a distância máxima para que essas duas fontes estejam minimamente resolvidas na tela.
Questão 13
Uma fonte de luz coerente e monocromática de comprimento de onda é utilizada num experimento cuja montagem está esquematizada na figura abaixo. As distâncias entre os anteparos consecutivos é . Luz incide normalmente sobre o anteparo , que possui duas fendas e , com mesma abertura e separadas por um distância . A distância é tal que os primeiros máximos laterais de interferência se localizem sobre as fendas e do anteparo . Elas possuem a mesma abertura das fendas do anteparo , mas estão separadas por uma distância .
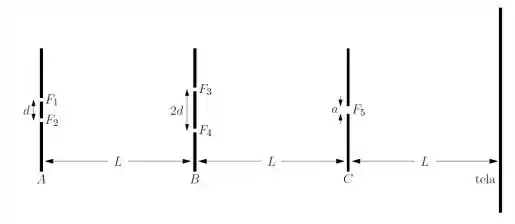
a) Quais são as diferenças de fase entre as ondas provenientes de e quando atingem as fendas e ?
b) Qual é o valor da separação em milímetros?
c) Qual é o valor limite da abertura (em milímetros) da fenda para que se possa distinguir dois máximos de difração (provenientes das fendas e ) na tela?
Ver solução completaQuestão 14
Duas fontes de luz são vistas à distância . A abertura da pupila do olho do observador tem diâmetro . Se os olhos do observador são perfeitos, a única limitação para a resolução das duas fontes é a difração.
Neste limite, qual será a distância entre as fontes, de modo que ainda consigamos vê-las como entidades separadas?
Considere , de modo que .
Nenhuma das anteriores
Ver solução completaQuestão 15
Qual é a separação linear entre dois objetos na superfície de Marte que podem ser resolvidos pelo telescópio Hubble com uma abertura ?
Dados:
A disância entre a Terra e Marte
O comprimento de onda da luz é
Ver solução completaQuestão 16
Duas fontes pontuais de luz estão afastadas de . Elas são vistas pelo olho a uma distância .
A abertura de entrada (pupila) do olho do observador tem um diâmetro . Se o olho é perfeito, o fator limitante para a resolução das duas fontes seria a difração.
Nesse limite, quão grande poderíamos fazer e ainda assim ver as fontes como entidades separadas?
Questão 17
Um observador na Terra, munido de uma luneta astronômica de diâmetro procura identificar estruturas geológicas na superfície de um planeta a uma distância da Terra .
A luneta contém filtros ópticos que, agindo separadamente, permitem observar luz de , e .
A menor distância , em quilômetros, entre duas estruturas geológicas na superfície do planeta, para que elas possam ser distinguidas pelo observador na Terra, quando a luneta estiver equipada com o fitro óptico amarelo é igual a...?
Para que tenhamos a possibilidade de enxergar duas estruturas que estejam a uma distância menor que , precisamos colocar um filtro de cor igual a...?
Ver solução completa