Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.6 - Ex. 52
Dois riachos se unem para formar um rio. Um dos riachos tem um largura de , uma profundidade de e a velocidade da água é . Outro riacho tem de largura , de profundidade e a velocidade da água é . Se o rio tem uma largura de e a velocidade da água é qual é a profundidade do rio?
Passo 1
Falaaa galerinha do RespondeAá, tudo beleza?
Nesse exercício aqui, temos dois riachos, um com largura de , profundidade de e velocidade da água , e o segundo riacho com de largura e de profundidade com velocidade da água de . Esses dois riachos se unem em determinado ponto para formar um rio, sabendo que o rio tem uma largura de e velocidade de , o enunciado quer que a gente encontre a profundidade do rio.
Belezoca, primeiramente, quando um fluido incompressível (densidade () constante) passa por seções transversais de áreas e com velocidades iguais a e (respectivamente), e o escoamento é estacionário (velocidade do fluido em cada ponto dele é constante) a seguinte igualdade ocorre:
Nada além do princípio da continuidade, caso tenha achado muita informação haha!
Passo 2
Vamos aplicar o conceito por trás da equação da continuidade nessa questão. Para isso, precisamos lembrar que essa equação denota a conservação da massa de um fluido que escoa por um sistema de forma estacionária e incompressível.
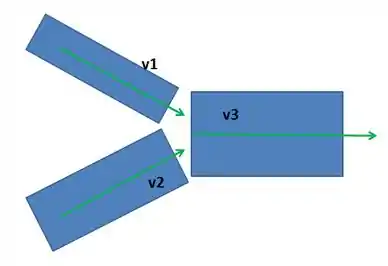
Assim, considerando que a soma das massas de fluido que passam pelos dois riachos iniciais com velocidades e deve ser igual à massa de fluido que atravessa o rio com velocidade , temos:
Sendo a massa de fluido que passa no riacho 1, a massa de fluido que passa no riacho 2 e a massa de fluido que passa no rio.
Passo 3
Com isso a vazão também deve ser conservada!! Logo, tudo o que passar pelos riachos 1 e 2 devem passar pelo rio. Isso nos diz que a vazão no rio deve ser igual à soma das vazões dos riachos 1 e 2.
Assim, temos, pela continuidade:
Onde , e são as áreas transversais de cada rio.
Para calcular a área, fazemos a largura de cada rio vezes a sua profundidade:
Onde é a profundidade do rio. Dessa forma:
Isolando na expressão acima, encontramos: