Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 83

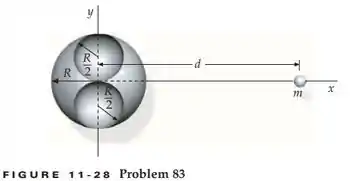
Duas cavidades esféricas idênticas são feitas em uma esfera de chumbo de raio R . Cada cavidade tem raio R / 2 . Cada cavidade tem raio R / 2 . Elas tocam a superfície da espera e seu centro, como na figura 11-28. A massa da esfera maciça e homogênea de chumbo, de raio R , é M . Determine a força de atração sobre uma partícula pontual de massa m localizada a uma distância d do centro da esfera de chumbo, como mostrado.

Passo 1

Quando temos cavidades a nossa estratégia é trabalhar com superposição. Basicamente vamos considerar o efeito da esfera completa e descontar o das cavidades, sacou?!

F r e s → = F 1 → - F 2 → - F 3 →

Onde F 1 → é devido a esfera completa e F 2 → e F 3 →   é efeito que as esferas de raio R / 2 iriam fazer.

Passo 2

Para F 1 → , temos seguinte:

F 1 →   = - G M m d 2 i ^

Como as cavidades são idênticas, o modulo de F 2 → e F 3 → são iguais. O triangulo retângulo para acharmos a distncia entre o centro da cavidade e a particulo é essa aqui ó:

  F 2 → = F 3 → = G M c a v m d 2 + R 2 2

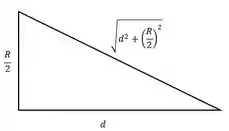
Para achar a massa da cavidade vamos fazer o seguinte:

ρ = M 4 3 π R 3 = M c a v 4 3 π R 2 3 → M c a v = M 8

Logo,

  F 2 → = F 3 → = G M m 8 ⋅ ( d 2 + R 2 2 )

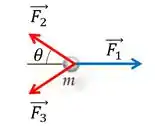
Decompondo os vetores vermelhos:

F x =   F 2 → cos ⁡ θ +   F 3 → cos ⁡ θ = G M m 8 ⋅ ( d 2 + R 2 2 ) ⋅ 2 c o s ⁡ ( θ ) F y =   F 2 → sen ⁡ θ -   F 3 → sen ⁡ θ = 0

Então,

F x = G M m ⋅ c o s ⁡ ( θ ) 4 ⋅ ( d 2 + R 2 2 )

Para o cos ⁡ θ :

cos ⁡ θ = d d 2 + R 2 2

Logo,

F x = G M m 4 ⋅ ( d 2 + R 2 2 ) ⋅ d d 2 + R 2 2

Passo 3

Agora vamos somar os vetores vermelho e azul!

F 1 →   = - G M m d 2 i ^

F 2 → + F 3 → = - G M m 4 ⋅ ( d 2 + R 2 2 ) ⋅ d d 2 + R 2 2 i ^

Repara que é negativo, pois aponta para o lado negativo do eixo x ! Agora vamos achar a resultante.

F r e s → = F 1 → - F 2 → - F 3 →

F r e s → = - G M m d 2 i ^ - - G M m 4 ⋅ ( d 2 + R 2 2 ) ⋅ d d 2 + R 2 2 i ^

Colocando - G M m d 2 em evidência:

F r e s → = - G M m d 2   1 + d 3 4 d 2 + R 2 4 3 2 i ^

Resposta

F r e s → = - G M m d 2   1 + d 3 4 d 2 + R 2 4 3 2 i ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra fina e homogênea de 20k g , com 5,0m de comprimento, é dobrada em um semicírculo. Qual é a força gravitacional exercida pela barra sobre uma massa pontual de 0,10k g localizada no centro da
Além de estudar amostras da superfície lunar, os atronautas da Apolo tiveram várias maneiras de determinar que a Lua não é feita de queijo. Dentre estas maneiras estão as medidas da aceleração da grav
Uma esfera homogênea de massa M está localizada próximo a uma barra fina e homogênea de massa m e comprimento L , como na figura 11-31. Determine a força gravitacional de atração exercida pela esfera
(a) Um anel fino e homogêneo, de massa M e raio R , está no plano x = 0 e centrado na origem. Esboce o gráfico do campo gravitacional g , versus x para todos os pontos no eixo x . (b) Em qual ponto, o
Dentro de uma esfera de raio R e de densidade ρ existe uma cavidade esférica de raio a . A distância entre os centros O e O ' da esfera e da cavidade é d . (a) Para um ponto P externo, alinhado com os