Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 104
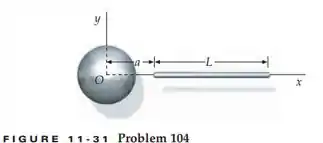
Uma esfera homogênea de massa está localizada próximo a uma barra fina e homogênea de massa e comprimento , como na figura 11-31. Determine a força gravitacional de atração exercida pela esfera sobre a barra.
Passo 1
Vem comigo que essa a gente vai matar no peito e chutar pro gol! Primeiramente, sabemos que o campo devido a esfera fora dela é o seguinte:
, onde x é a distância até o ponto
Passo 2
Agora vamos considerar um pedacinho da barra de massa a uma distância do centro. Logo,
Como estamos trabalhando com uma barra:
, onde
Passo 3
Por fim, vamos integrar do começo da barra até o final :
Isto é,
Portanto,
Resposta
Exercícios de Livros Relacionados
Como geólogo de uma companhia de mineração, você esta trabalhando em um método de determinação de possíveis locais de depósitos minerais subterrâneos. Suponha que a crosta da Terra tenha a espessura d
Um túnel reto é cavado através de um planeta esférico com massa específica de massa ρ 0 . O túnel passa pelo centro do planeta e é perpendicular ao eixo de rotação do planeta, que é fixo no espaço. O
Duas cavidades esféricas idênticas são feitas em uma esfera de chumbo de raio R . Cada cavidade tem raio R / 2 . Cada cavidade tem raio R / 2 . Elas tocam a superfície da espera e seu centro, como na
Um agregado globular é uma coleção aproximadamente esferica de até milhões de estrelas ligadas pelo força da gravidade. Os astrônomos medem as velocidades das estrelas no agragado para estudar sua com
A massa específica de uma esfera é dada por ρ r = C / r . A esfera tem um raio de 5,0m e uma massa de 1,0 × 10 11k g . (a) Determine a constante C . (b) Obtenha expressões para o campo gravitacional n