Procurando um buraco negro. As observações da luz de uma estrela indicam que a estrela faz parte de um sistema binário (sistema de duas estrelas). A estrela visível do par tem uma velocidade orbital , um período orbital dia e uma massa aproximada , onde é a massa do sol . Suponha que as órbitas da estrela e da companheira, que é escura e invisível, são circulares. Qual é a massa da estrela escura, em unidades de .
Passo 1
Fala galerinha bonita, tudo beleza?
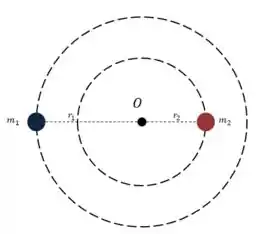
No ponto da figura, temos o centro de massa do sistema binário. Perceba que as duas estrelas estão orbitando esse ponto em uma trajetória circular. Vamos pensar na estrela mais externa primeiro.
Se ela é mantida em órbita circular, é porque existe uma força centrípeta que mantém ela nessa trajetória. Nesse caso, é a força gravitacional exercida pela estrela mais interna:
Na fórmula da força, o é a distância entre uma estrela e outra, há na força centrípeta, é o raio da órbita da estrela mais externa.
Agora precisamos encontrar uma relação entre e .
Passo 2
Pela fórmula do centro de massa sabemos que:
Olhando para a figura, temos que:
Substituindo o resultado anterior aqui:
Ou seja:
Passo 3
Agora podemos usar o período e a velocidade da estrela mais externa para substituir e, consequentemente, . Em um órbita circular:
Substituindo isso na equação anterior:
Agora nossa equação inicial:
Vira:
Passo 4
Agora precisamos arrumar essa confusão!
Resolvendo as potências e organizando as frações:
Agora vamos cortar o que for possível:
Agora vamos tentar isolar as massas, que é o que nos interessa:
Beleza, temos todos os valores do lado direto, é só convertermos o período para segundos e podemos começar a substituir:
Agora vamos ao passo final:
Passo 5
O enunciado pede a resposta em termos de massas solares , e já sabemos que:
Substituindo:
Dá pra facilitar bastante se escrevermos , ou seja, escrevermos como algum múltiplo de . Aí fica:
Aí caímos em uma equação do terceiro grau:
Usando algum método numérico ou um computador, podemos encontrar a solução real: