Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.5 - Ex. 42
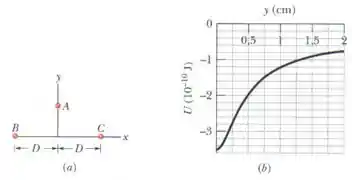
A figura (a) mostra uma partícula que pode ser deslocada ao longo de um eixo desde uma distância infinita até a origem. A origem está localizada no ponto médio entre as partículas e , que têm massas iguais, e o eixo é perpendicular à reta que liga essas duas partículas. A distância é . A figura (b) mostra a energia potencial do sistema de três partículas em função da posição da partícula no eixo . A curva na verdade se estende indefinidamente para a direita e tende assintoticamente para um valor de quando . Qual é a massa (a) das partículas e e (b) da partícula .
Passo 1
(a) Vamos enfatizar que o gráfico da figura (b) representa a energia potencial do sistema de três partículas. Isso significa que a quantidade do gráfico é calculada somando as energias potenciais entre cada par de partículas, da seguinte forma:
Quando aumenta (no gráfico), a partícula está se afastando das outras duas. Perceba que:
Ou seja, todos os potenciais que envolvem a partícula se anulam, e sobra apenas:
Passo 2
O enunciado nos disse que as massas e são iguais, e pela figura vemos que
Substituindo na fórmula para quando :
Multiplicando por , cortando a potência e isolando o que queremos obter:
Ajustando os algarismos significativos:
Passo 3
(b) Agora, queremos encontrar a massa da partícula . Vamos ver as informações que nós já temos:
Veja que ainda não usamos nenhuma informação do gráfico! Se pegarmos um ponto conveniente ali, podemos usar a primeira equação para calcular .
O ponto que mais facilita nossa vida tem e . Nesse caso:
Resolvendo a equação acima:
Multiplicando tudo por e dividindo por :
Colocando em evidência:
Agora substituindo os valores:
Ajustando para dois algarismos significativos:
Pronto!
Resposta
(a)
(b)