Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 40
As duas fontes sonoras do Problema 39 estão agora fora da fase 90°, mas com a mesma frequência do Problema 39. Em que ângulos são ouvidas interferências construtivas e destrutivas?
Passo 1
Bom, como temos uma fase entre as duas fontes e também temos uma fase causada pela diferença entre os caminhos percorridos pelas ondas de cada fonte, vamos escrever a equação do ângulo de fase da seguinte maneira:
Onde corresponde à fase pela diferença de caminhos e corresponde à fase entre as fontes
Passo 2
Pela equação da fase pela diferença entre os caminhos:
E substituindo os 90° dados no enunciado, a nossa equação pra fase total fica:
Como buscamos os ângulos onde há interferências construtivas, então deve ser:
E resolvendo para , ficamos com:
Passo 3
E pela relação entre e d:
Utilizando e do Problema 39, e isolando :
Para cada m teremos um angulo onde há interferência construtiva, vamos então montar uma tabela:
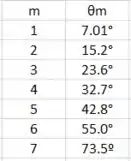
Para m>7, o arco seno não está definido.
Passo 4
E para interferências destrutivas a condição para a fase do Passo 1 será:
Resolvendo para , ficaremos com:
Pela relação entre e d:
Isolando
Ficaremos com a seguinte tabela para os ângulos onde ocorrem interferências destrutivas:
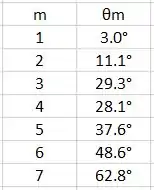
Resposta
Ei, a resposta está no passo a passo :)