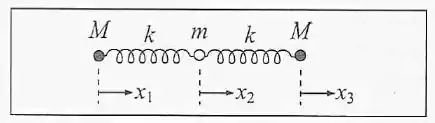
Um modelo clássico para a molécula de é constituído por duas partículas idênticas de massa ligadas a uma partícula central de massa por molas idênticas de constante elástica e massa desprezível. Sejam , e os deslocamentos das três partículas a partir das respectivas posições de equilíbrio (figura). (a) Escreva as equações de movimento para , e e verifique que o centro de massa do sistema permanece em repouso ou em movimento retilíneo uniforme. (b) Obtenha as equações de movimento para a as coordenadas relativas, e . (c) A partir de (b), calcule as frequências angulares de oscilação associadas aos dois modos normais de vibração do sistema. Interprete fisicamente estes dois modos, caracterizando os tipos de oscilação das massas a eles associados. (d) Aplique este modelo à molécula de , calculando a razão entre as duas frequências de modos normais de vibração para esta molécula. Tome as massas do carbono e oxigênio como e , respectivamente, em unidades de massa atômica.
Passo 1
Vamos começar escrevendo a segunda lei de Newton para cada uma das molas.
No caso da mola da esquerda, por exemplo:
E usando a lei de Hooke (, a força vai ser proporcional ao comprimento daquela primeira mola:
É só usar a mesma lógica para as outras molas, e você vai ficar com essas expressões aqui:
E o enunciado pediu pra mostrar que o centro de massa fica parado ou em movimento retilíneo uniforme.
Lembra da fórmula para a posição do centro de massa?
A gente pode derivar isso duas vezes em relação ao tempo pra encontrar a aceleração do centro de massa:
E aí é só substituir com aquelas fórmulas lá de cima:
E todos os termos do numerador vão se cancelar!
Então o centro de massa não tem aceleração! Ele se mantém parado ou em movimento retilíneo uniforme.
Passo 2
(b) Agora vamos olhar de novo pro sistema lá do passo :
Reorganizando um pouco:
Pra simplificar mais ainda, vamos inventar duas variáveis novas:
Então:
Nosso objetivo aqui é escrever isso tudo em função das duas variáveis que o enunciado deu:
Passo 3
Se a gente subtrair a primeira equação da segunda, vai sair o seguinte:
E aqui já dá pra ver o e o aparecendo:
E agora vamos subtrair a segunda da terceira:
Vamos fazer as mesmas substituições com o e o :
Beleza, agora ficamos com só duas equações ao invés de três:
Passo 4
(c) O próximo passo é calcular as frequências angulares de oscilação usando essas equações:
O problema é que essas equações ainda tem duas variáveis cada! Vamos ter que introduzir mais um par de variáveis novas pra resolver isso:
Se a gente somar as duas equações do sistema:
E agora é só substituir o aí no meio:
Simplificando um pouco:
E se a gente subtrair a primeira equação da segunda:
E agora vamos substituir o :
Agora sim, ficamos com um sistema de duas equações de uma variável cada:
A interpretação física é a seguinte:
No primeiro modo, as partículas estão oscilando em relação ao centro geométrico do sistema (que é justamente o que a coordenada representa). E as duas massas das extremidades vão ter amplitudes opostas.
No segundo modo, e massa que fica no meio está oscilado em relação ao centro de massa do sistema.
Passo 5
Essas duas equações já estão na forma do oscilador harmônico:
Então a frequência da primeira equação é:
E a da segunda equação é:
Passo 6
(d) E a nossa última tarefa é calcular a razão entre essas frequências, usando esses valores aqui:
A razão é:
Simplificando um pouco:
Resposta
(a) As equações de movimento são .
(b) As novas equações são , com e .
(c) As duas frequências de oscilação são e .
(d) A razão entre as duas frequências é .