Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 6
|| Um ônibus espacial encontra-se em órbita acima da superfície terrestre.
Qual é a força gravitacional exercida sobre uma esfera de no interior do ônibus espacial?
A esfera flutua no interior do ônibus espacial, aparentemente “sem peso”. Como isso é possível?
Passo 1
Esse capítulo se dedica a estudar gravitação, em especial para os corpos celestes. Tudo está relacionado através do que os físicos chamam Lei da gravitação universal basicamente temos que ter em mente que:
A lei da Gravitação universal diz:
“Se dois corpos possuem massa, ambos estão submetidos a uma força de atração mútua proporcional às suas massas e inversamente proporcional ao quadrado da distância que separa seus centros de gravidade.”
Matematicamente:
Só tome cuidado com o , ele é a Constante Gravitacional Universal (), ele não é a gravidade que estamos acostumados!!
O mais incrível é que isso é aplicado para tudo o que existe! Por exemplo: A força do Sol sobre os planetas é idêntica à força da Terra sobre nós. Numa abordagem mais imaginativa vc tb pode pensar que tudo que possui massa se atraem, mas claro, só corpos com massas absurdamente altas tem um efeito notável.
Parece imaginação, mais é um bom método para calcular dados reais. A Estação Espacial internacional (ISS), por exemplo, leva em conta a lei da gravitação universal para poder orbitar a nossa Terra! E vc pode ver isso em tempo real aqui (Desculpa Terraplanistas kkkk):
https://www.nasa.gov/multimedia/nasatv/iss_ustream.html
Passo 2
Você precisa conhecer alguns dados antes de resolver essa questão. Apesar deles não estar na questão, eles foram apresentados no livro texto desse capítulo, lembre-se:
Massa da Terra:
Circunferência da Terra pelo Equador:
Raio da Terra aproximado:
Passo 3
Qual é a força gravitacional exercida sobre uma esfera de no interior do ônibus espacial?
Veja a nave está a acima da superfície terrestre, mas a distancia até o centro da Terra tb tem que ser considerado, para podermos usar a Lei da gravitação (A referencia para distância é o centro de gravidade). Observe esquema, para o problema:
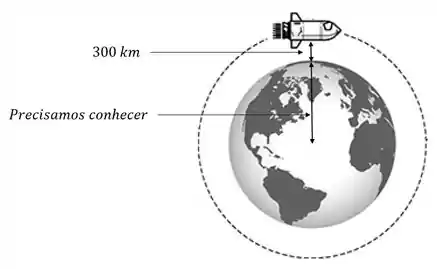
O que precisamos conhecer aqui é o raio da Terra, que é aproximadamente . Claro que estamos considerando aproximações. Até por que a terra não é um globo perfeito. Além desse vamos precisar saber a massa da Terra tb.
Tranquilo agora podemos aplicar a Lei da gravitação Universal, considerando a distância até o centro de gravidade entre ambos os corpos... Mas como o centro de gravidade da nave não é astronômico, ele se torna insignificante e não precisamos leva-lo em consideração, ficamos:
Passo 4
A esfera flutua no interior do ônibus espacial, aparentemente “sem peso”. Como isso é possível?
Uma reposta direta é: Flutuam por que os corpos em orbita estão em queda livre.
Veja uma explicação mais detalhada: O que acontece é que os corpos em orbitas executam um movimento de queda livre.( movimento resultante unicamente da aceleração provocada pela gravidade, ocorre atração gravitacional), mas vc poderia pensar, e por que eles não se chocam na superfície terrestre? E a resposta é: Ao mesmo tempo em que está caindo em direção à Terra, as naves e os satélites se move com velocidade orbital em uma direção tangencial (e é velocidade muito rápida, cerca de ). Então há uma espécie de equilíbrio. Veja essa animação como é movimento se estiver dúvidas:
https://bit.ly/2YiBn7q
Veja que não é devido a “falta de gravidade”. Essa afirmação é um erro. Na maioria das vezes dizemos isso, mas não está correto. A gravidade nessa condição não é zero! Inclusive a a força gravitacional é apenas 10% menor que a força gravitacional da superfície terrestre.
Resposta
Flutuam por que os corpos em orbita estão em queda livre.