Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 58

Uma ponte levadiça homogênea deve ser mantida suspensa a um ângulo de 30 ° acima da horizontal, para permitir que os navios passem por baixo dela. A ponte pesa 45000 N e tem 1,40 m de comprimento. Um cabo é conectado a 3,5 m da dobradiça em torno da qual a ponte gira (conforme medido ao longo da dobradiça) e puxa horizontalmente a ponte para mantê-la fixa. a) Qual é a tensão no cabo? b) Ache o módulo, a direção e o sentido da força que a dobradiça exerce sobra a ponte.

Passo 1

Precisamos aplicar a primeira e a segunda condições de equilíbrio na ponte levadiça. Mas antes, vamos esboçar o diagrama de corpo livre da levadiça:

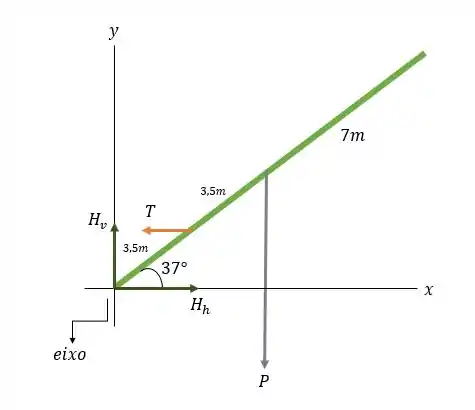
H v e H h são os componentes da força que a dobradiça exerce na ponte.

Passo 2

  1. Então, aplicando ∑ τ = 0     com o eixo na dobradiça:

    2. - P ( 7 m ) ( cos ⁡ 37 ° ) + T ( 3,5 m ) ( sen ⁡ 37 ° ) = 0

    E isso implica que:

    T = 2 P   cos ⁡ 37 ° sen ⁡ 37 ° = 45 N tan ⁡ 37 ° = 1,19 × 10 5 N

    Passo 3

  2. E aplicando a segunda condição:

∑ F x = 0

H h = T = 1,19 × 10 5 N

E

∑ F y = 0

H v = P = 4,50 × 10 4 N

E então,

H = H h 2 + H v 2 = 1,27 × 10 5 N

E para encontrar a direção, fazemos que:

tan ⁡ θ = H v H h

Dessa forma, temos que θ é dado por:

θ = tan - 1 ⁡ θ = 20,7 °

Resposta

  1. T = 1,19 × 10 5 N
  2. A força da dobradiça tem magnitude 1,27 × 10 5   N e é direcionado a 20,7 ° acima da horizontal.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas vigas idênticas e uniformes, pesando 260 N cada, estão ligadas em uma extremidade por uma dobradiça de atrito desprezível. Uma barra transversal leve presa no meio das vigas mantém um ângulo de 5
Você deseja fazer uma roda de bicicleta de massa m e raio R subir um desnível de altura h. Para fazer isso você aplica uma força horizontal F → (Figura 11.52). Qual é o menor módulo dessaforça para fa
Um poste uniforme de uma linha de transmissão possui 9,0 m de comprimento e pesa 5700 N. Antes de ser instalado em seu buraco, ele faz um ângulo diferente de zero com a vertical. Umcabo vertical ligad
O portão de uma fazenda. Um portão de 4,0m de largura e 2,0m de altura pesa 500N . Seu centro de gravidade está localizado em seu centro, e ele está articulado nos pontos A e B . Para avaliar a tensão
A porta de uma garagem é apoiada sobre um trilho superior (Figura 11.59). As rodas A e B enferrujaram, portanto não giram mais, podendo apenas deslizar ao longo do trilho. O coeficiente de atrito está