Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 78
Para a esfera com cavidade do problema 77, mostre que o campo gravitacional é uniforme dentro da cavidade e determine sua magnitude e orientação.
Passo 1
Vem com calma que essa é cascuda! Aqui eu botei uma representação da cavidade:
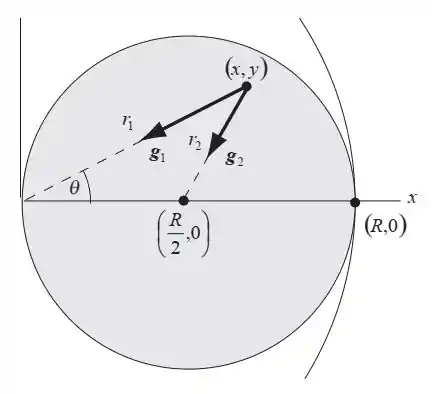
Nessa imagem a gente vê , que é o campo gerado pela esfera maior, que é o campo gerado pela esfera menor. Esse da esfera menor, como vimos na questão anterior, vai ser um “anti-campo” gerado pela massa negativa que consideramos que essa esfera tem.
Passo 2
Sendo a densidade volumétrica das esferas, vamos calcular o campo gravitacional de cada uma delas!
Primeiro :
Esse é o módulo de , mas o campo gravitacional é vetorial! Então vamos escrever como uma soma das componentes horizontal e vertical, usando aquele ângulo da figura como referência.
Vamos pensar em cada uma dessas componentes separadas, com auxílio da figura:
Esse sinal negativo aparece porque o campo é atrativo, então aponta pra dentro, sacou? Então vai ser:
Passo 3
Vamos fazer o mesmo procedimento para agora, fazendo aquela brincadeira de considerar a massa dele negativa, por ser uma cavidade!
Esse é o módulo de , mas o campo gravitacional é vetorial! Então vamos escrever como uma soma das componentes horizontal e vertical, usando agora o ângulo que a linha de até o centro faz com a horizontal.
Vamos pensar em cada uma dessas componentes separadas, com auxílio da figura:
Passo 4
Agora é só somar as duas!
Então o módulo de é:
Resposta
O campo gravitacional é orientado no eixo , com direção para o centro da esfera maior.