Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 87

Um ioiô de 0.10 k g consiste em dois discos maciços, cada um de 10 c m de raio, ligados por uma haste sem massa de 1,0 c m de raio. Um fio está enrolado em volta da haste. Uma extremidade do fio é mantida fixa e, enquanto o ioiô cai, o fio está tensionado. O ioiô gira, ao descer verticalmente. Determine (a) a aceleração do ioiô e (b) a tensão T.

Passo 1

a) Oláaaa, querido!

Temos um ioiô caindo. Ele quer saber a aceleração linear a dele durante a queda.

Se a gente precisa achar a aceleração, é uma boa usar a segunda lei de Newton aqui. E se tem segunda lei de Newton, precisamos do diagrama de corpo livre do ioiô:

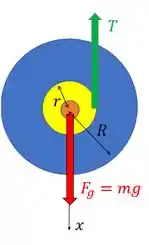
Essa parte azul representa os dois discos maciços e parte amarela representa a haste.

Repara que temos duas forças atuando. A força peso F g do ioiô que não causa torque porque a linha de ação dela passa pelo centro de massa do ioiô.

E temos a força de tensão no fio que envolve o ioiô. Ela está sendo aplicada no que o enunciado chama de haste, que tem raio r = 1   c m = 0 , 0 1   m . Essa haste é a parte do ioiô onde a corda fica enrolada.

Então bora lá aplicar a segunda lei de Newton para achar aceleração desse cara.

Passo 2

Podemos aplicar a segunda lei de Newton para o centro de massa do ioiô. Colocamos o referencial no diagrama que coloca x positivo no sentido da aceleração do ioiô. Aí ficamos assim:

∑ F x = m a x

F g - T = m a

m g - T = m a

T = m g - a   i

Não temos nem T nem a , então precisamos de mais uma equação para achar a .

Passo 3

Como o ioiô gira, a gente pode aplicar aqui a segunda lei de Newton para a rotação também:

∑ τ = I α

A única força que gera torque no ioiô é a tensão T que não tem linha de ação passando pelo CM do ioiô. E como essa força é sempre perpendicular ao raio r da haste e está aplicada a essa distância do eixo de rotação no centro do ioiô, o torque gerado vale

τ = T r

E aí a segunda lei fica

T r = I α

A gente pode relacionar a aceleração linear a do ioiô com sua aceleração angular α   usando essa expressão:

a = r α → α = a r

Substituindo a nossa equação

T r = I a r

Passo 4

E I é o momento de inércia do ioiô de massa m = 0,1   k g . Ele é formado por dois discos com massa e a haste sem massa. Então a gente pode dizer que o momento de inércia só vai levar em conta os discos. Ambos com o eixo de rotação passando pelo seu centro.

Então o momento de inércia do nosso ioiô vai ser a soma dos momentos de cada disco de massa m / 2 . Um disco tem momento de inércia em relação ao seu centro é

I d i s c o = M R 2 2

Esse é igual ao momento de inércia de um cilindro. Então dois discos de massa M = m / 2 e raio R tem momento de inércia:

I = 1 2 m 2 R 2 + 1 2 m 2 R 2

I = m R 2 2

Substituindo na nossa equação

T r = I a r

T r = m R 2 2 a r   i i

Passo 5

Aí a gente tem duas equações e duas incógnitas. Podemos achar a :

T = m g - a   i

T r = m R 2 2 a r   i i

Substituindo a primeira na segunda:

m g - a r = m R 2 2 a r

Arrumando

m g - m a = m × R 2 r 2 a

Dividindo tudo por m e e isolando a

a R 2 2 r 2 + 1 = g

a = g 1 + R 2 2 r 2

Substituindo os valores numéricos que já temos:

a = 9.81 1 + 0.10 2 2 × 0.01 2

a = 0.192   m / s 2

Passo 6

b) Como queremos a tensão T e temos a aceleração a , podemos usar a expressão i e achar T :

T = m g - a

Agora é só substituir nossos valores:

T = 0.10 9.81 - 0.192

T = 0.96 N

Resposta

  1. a = 0.192 m s 2
  2. T = 0.96 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A polia indicada na Figura 9.36 possui raio 0,160 m e momento de inércia 0,480k g ⋅ m 2 . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocida
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,
Uma fita leve está enrolada em volta de um disco circular de massa m e raio r , que rola sem deslizar sobre um plano inclinado áspero de inclinação θ . A fita passa por uma roldana fixa de massa despr
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
No cilindro junto com a massa do Exemplo 9.9 (Seção 9.4), suponha que a massa m que cai seja feita de borracha, de modo que nenhuma energia mecânica é perdida quando a massa atinge o solo. a) Supondo