Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 37.Exercícios - Ex. 22

Uma espaçonave inimiga esta perseguindo sua espaçonavee Starfighter com velocidade, medida em relação a você, igual a 0,400 c. A espaçonave inimiga dispara um míssil para atingir a Starfighter com um velocidade, em relação à espaçonave inimiga, de 0,700 c (Figura 37.28).

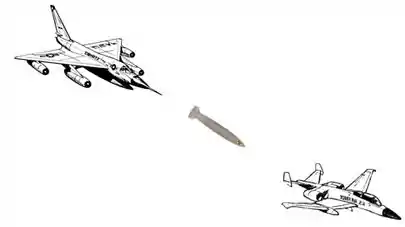
  1. Qual a velocidade do míssil em relação a você? Expresse sua resposta em termos da velocidade da luz.
  2. Se você mediu uma distância igual a 8,0   x   10 6   k m entre você e a espaçonave inimiga no instante em que o míssil foi disparado, qual será o tempo que o míssil levará para atingir você?

Passo 1

Dados:

u = 0,400 c

v ' = 0,700 c

Passo 2

  1. A velocidade do míssil em relação ao observador será calculada a partir da equação

    2. v = v ' + u 1 + u v ' / c 2

    Substituindo os termos

    v = 0,700 c + 0,400 c 1 + ( 0,400 ) ( 0,700 ) = 0,859 c

    Passo 3

  2. O tempo que o míssil levará para atingir até o observador pode ser calculado através da quação da velocidade média.

v = ∆ s ∆ t

Isolando ∆ t e substituindo os termos, temos.

OBS: A VELOCIDADE DEVE SER MULTIPLICADA PELA VELOCIDADE DA LUZ NO VÁCUO.

t = 8   x   10 9 0,859 3   x   10 8

t = 31   s

Resposta

  1. 0,859 c
  2. t = 31   s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma nave espacial de comprimento adequado Lp = 400 m passa por uma estação transmissora a uma velocidade de 0,760c. (A estação transmissora transmite sinais que viajam à velocidade da luz.) Um relógio
No referencial S, os eventos 1 e 2 são separados por uma distância D = x2 - x1 e um tempo T = t2 - t1. (a) Use a transformação de Lorentz para mostrar que no referencial S ′, que está se movendo ao lo
Um foguete com comprimento adequado de 700 m está se movendo para a direita a uma velocidade de 0,900c. Ele tem dois relógios - um no nariz e outro na cauda - que foram sincronizados na estrutura do f
Uma longa haste paralela ao eixo x é liberada do repouso. Subsequentemente, ele está em queda livre com uma aceleração de magnitude g na direção –y. Um observador em um foguete se movendo com velocida
A equação para a frente de onda esférica de um pulso de luz que começa na origem no tempo t = 0 é x2 + y2 + z2 - (ct) 2 = 0. O quadro S ′ se move com velocidade v ao longo do eixo x. Usando a transfor