(b) Existe uma interpretação geométrica da equação , baseada no teorema de Pitágoras. Desenhe um triângulo ilustrando esta interpretação.

(b) Bom! O problema pede para desenhar um triângulo.Então, vamos desenhar um triângulo.A seguinte interpretação geométrica pedida na questão, pode ser descrita, analisando a imagem abaixo:

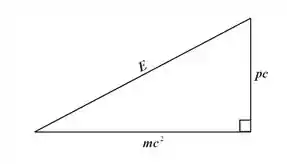
Bom! O teorema de Pitágoras, mais conhecido teorema do mundo, diz que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa em um triângulo retângulo. Vamos então, aplicá-lo ao nosso triângulo, considerando que ele se enquadra nesse caso:

Achamos assim, que:

Ihhh! Olha lá! Achamos pelo teorema de Pitágoras a seguinte fórmula: , que é igualzinha à fórmula que queríamos descrever através de uma interpretação geométrica no enunciado. Logo, o triângulo retângulo é a figura geométrica mais adequada para descrever essa relação