Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 13.Problemas - Ex. 91

Experimentando com pêndulos, você prende um fio leve ao teto e uma pequena esfera de metal à ponta inferior do fio. Quando você desloca a esfera por 2,00 m à esquerda, ela quase toca na parede vertical; com o fio esticado, você solta a esfera do repouso. A esfera oscila como um pêndulo simples, e você mede seu período T. Esse ato é repetido para fios de vários tamanhos L, cada vez começando o movimento com a esfera deslocada 2,00 m à esquerda da posição vertical do fio. Em cada caso, o raio da esfera é muito pequeno em comparação com L. Seus resultados são dados na tabela a seguir:

(a) Para os cinco maiores valores de L , represente graficamente T 2   v e r s u s   L . Explique por que os pontos de dados ficam próximos de uma linha reta. A inclinação dessa linha tem o valor que você esperava? (b) Acrescente os dados restantes ao seu gráfico. Explique por que os dados começam a se desviar da linha reta à medida que L diminui. Para ver esse efeito mais claramente, desenhe o gráfico de T / T 0 versus L , onde T 0 = 2 π L / g e g   =   9,80   m / s 2 . (c) Use seu gráfico de T / T 0 versus L para estimar a amplitude angular do pêndulo (em graus) para a qual a equação T = 2 π L / g tem um erro de 5%.

Passo 1

Faaaaala meu povo, bora iniciar mais um livrinho com a gente!

Letra a)

Bem pessoal, pra essa questão temos que a equação que estabelece o período T e o comprimento do pêndulo L é:

T = 2 π L g

T 2 = 2 π 2 L g  

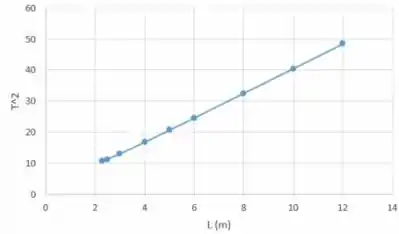
Se plotarmos os dados fornecidos onde a equação:

T 2 = 2 π 2 L g  

Controla o gráfico, o gráfico é mostrado abaixo. Onde a inclinação é 2 π 2 g . O gráfico é uma linha reta.

Passo 2

Letra b)

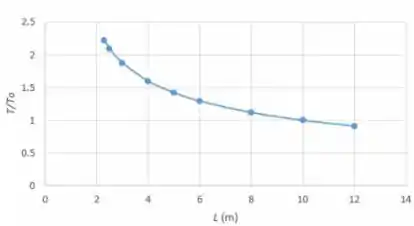
O gráfico para T / T 0 versus L é mostrado abaixo. Os dados desviam da linha reta porque o deslocamento é pequeno em um comprimento grande e como o comprimento é muito pequeno, o deslocamento não seria pequeno. Portanto, os dados se desviam da linha reta conforme mostrado abaixo.

Passo 3

Letra c)

A amplitude angular está relacionada ao comprimento do pêndulo pela próxima equação:

L sin ⁡ θ = 2   m

Assim, podemos obter θ por:

θ = arcsin ⁡ 2 m L

θ = arcsin ⁡ 2   m 2,5   m = 53,13 °

E assim acabamos nossa questão, deu tudo certinho aí? 😉 Te vejo na próxima!

Resposta

Letra a)

v e r   p a s s o   a   p a s s o

Letra b)

v e r   p a s s o   a   p a s s o

Letra c)

θ = 53,13 °

Exercícios de Livros Relacionados

81. Não perca o barco. Em visita a Minnesota (a ‘terra dos dez mil lagos’), você se inscreve em uma excursão ao redor de um dos maiores lagos. Ao chegar ao cais onde o barco de 1500k g está ancorado,
76. Um parafuso de 0,0200k g executa um M H S com amplitude igual a 0,240m e período igual a 1,500s . O deslocamento do parafuso é igual a + 0,240m quando t = 0 . Calcule: a ) o deslocamento do parafu
66. Uma criança travessa faz seu prato de jantar de 250g deslizar em uma mesa horizontal em M H S com amplitude 0,100m . Em um ponto situado a 0,060m da posição de equilíbrio a velocidade do prato é i
82. Um exemplo interessante de oscilação, embora impraticável, é o movimento de um objeto que é deixado cair em um furo que atravessa a Terra de um extremo ao outro, passando pelo centro. Usando a hip
85. Considere o círculo de referência indicado na Figura 13.6 . O componente x da velocidade do ponto Q é a velocidade do ponto P . Calcule esse componente e mostre que a velocidade do ponto P é dada