Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 92
Em um experimento para medir a distância entre a superfície da Terra e a superfície da Lua, a radiação pulsada de um laser de rubi () foi apontada para a Lua através de um telescópio refletor cujo espelho tinha um raio de . Um refletor deixado por astronautas na Lua se comportou como um espelho plano circular com de raio, refletindo a luz diretamente de volta para o telescópio. A luz refletida foi detectada depois de ser focalizada pelo telescópio. Aproximadamente que fração da energia luminosa original foi recebida pelo detecetor? Suponha que toda a energia dos feixes de ida e de volta esteja concentrada no pico central de difração.
Passo 1
Quando a luz emitida pelo laser na Tera chega até a lua, o se feixe vai ocupar uma certa região circular, certo? Vamos começar calculando o diâmetro dessa região:
Onde é o diâmetro do espelho do telescópio, e é o ângulo representado nesse desenho:
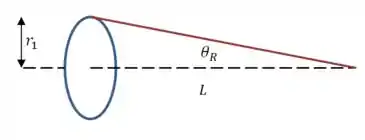
Podemos relacionar o raio , ou o diâmetro , com o ângulo :
Beleza, esse é o raio da região total ocupada pelo feixe que chega a lua.
Passo 2
Se o espelho deixado na lua tem raio , qual fração da área total do feixe que chega é ocupada pelo espelho?
Então essa é a fração da energia que o espelho aproveita.
Em seguida, a luz é refletida pelo espelho de diâmetro , o que significa que vai chegar na Terra como um feixe que tem diâmetro :
Onde usamos a exata mesma fórmula do passo anterior.
Dessa vez, o feixe de diâmetro vai ser capturado por um telescópio de raio , então a fração da energia aproveitada é:
Passo 3
Beleza, então temos que considerar as “perdas” de energia em dois passos: e .
Por isso, a fração da energia que é recebida de volta após todo o processo é:
Agora é só substituir todas as expressões que nós calculamos:
Agora elevamos tudo ao quadrado:
Então, sabendo que a distância da Terra até a Lua é de , vamos substituir os valores:
Resposta
A fração da energia luminosa original que foi recebida pelo detector é aproximadamente .