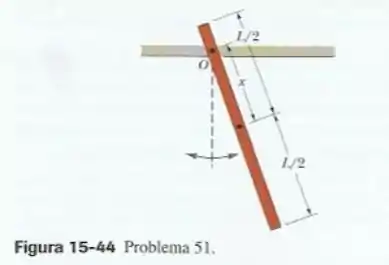
Na Fig. 15-44, uma barra de comprimento oscila como um pêndulo físico. (a) Que valor da distância entre o centro de massa da barra e o ponto de suspensão corresponde ao menor período? (b) Qual é esse período?

Falaaaa galerinha bonita, tudo beleza?

Esse exercício aqui é muito parecido ao exercício tratado no Problema Exemplo – “Período de comprimento de um pêndulo físico”, exceto que não é mais a extremidade da barra. Chamando de o centro de massa (assumindo que também seja o centro geométrico da barra), nós podemos ver que a distância entre e é . Aplicando o teorema dos eixos paralelos, a gente tem:

Sabendo do momento de inércia, a gente substitui na equação do período .

Beleza! Próximo passo, agora, é derivar e igualar a zero. Assim, a gente acha o mínimo da função. Minimizando a partir de gráficos é fácil, mas o método de calcular (igualando a derivada da função a zero) pode fornecer pontos que não são necessariamente mínimos da função. Pra facilitar nossa vida, como a dependência de x encontra-se somente dentro da raiz, vamos achar o mí imo da função que tá dentro da raiz quadrada.

Isso nos leva a