Uma onda senoidal que se propaga em uma corda é mostrada duas vezes na figura, antes e depois que o pico se desloque no sentido positivo de um eixo em . A distância entre as marcas do eixo horizontal é ; . Se a equação da onda é da forma , determine (a) , (b) , (c) e (d) o sinal que precede .
Passo 1
Falaaa galerinha bonita, tudo beleza?
Saca só, nesse exercício o enunciado nos deu uma onda senoidal que se propaga em uma corda em dois momentos diferentes, antes e depois que o pico se desloque de uma distância no sentido positivo de um eixo em .
E sabendo que a distância entre as marcas do eixo horizontal é e , dado a equação da onda , o enunciado pede pra gente encontrar, na era (a), amplitude do movimento.
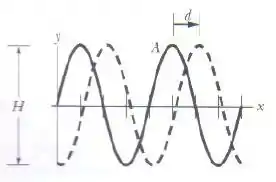
Belezoca, a amplitude é a altura dos picos da onda, ou a distância máxima que a onda atinge em relação ao eixo .
Se a gente reparar no gráfico, vamos ver que essa distância máxima é a metade daquela altura que está marcado do lado, afinal é distância máxima entre os extremos da corda, sendo assim:
Como vamos obter que:
Passo 2
Iradoso, agora na letra (b) queremos encontrar o número de onda , que segue essa fórmula aqui:
Onde é o comprimento de onda. Uma forma da gente encontrar esse comprimento do gráfico é contando a distância, no eixo , ocupada por um pico somado a um vale.
Como cada marca no eixo vale , e temos 4 marcas entre dois vales (ou dois picos), então o comprimento de onda será:
E então:
Passo 3
Show de bolinhas, já na letra (c) precisamos determinar o valor da frequência angular , pra isso vamos precisar da fórmula:
MAAASSS, aqui vamos precisar de toda malandragem, afinal o enunciado não nos deu informações tão diretas assim sobre a frequência , então podemos lembrar que:
Onde é a velocidade da onda que podemos medir através das informações do enunciado, já que ela percorre em , logo:
Sendo assim, será:
E como vimos que , obtemos que:
Portanto, a frequência angular é dada como:
Passo 4
Por último, na letra (d) o sinal que fica atrás do sempre depende do sentido em que a onda se propaga (nunca mais podemos esquecer disso), logo:
No nosso caso, o enunciado disse que a onda se propaga no sentido positivo, então tem um sinal negativo. Portanto:
Prontinho galera!

Resposta
(a)
(b)
(c)
(d) Negativo: