Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.4 - Ex. 40

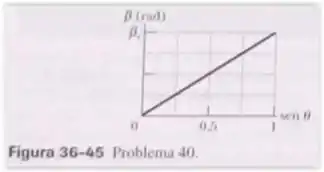
A Fig. 36-45 mostra o parâmetro β da Eq. 36-20 em função do seno do ângulo θ em um experimento de interferência de dupla fenda usando uma luz com um comprimento de onda de 435   n m . A escala do eixo vertical é definida por β s = 80,0   r a d . Determine (a) a distância entre as fendas, (b) o número de máximos de interferência (considerando os máximos de um lado, e do outro, o máximo central), (c) o menor ângulo para o qual existe um máximo e (d) o maior ângulo para o qual existe um mínimo. Suponha que nenhum dos máximos de interferência seja totalmente eliminado por um mínimo de difração.

Passo 1

A difração por uma rede de N ranhuras produz máximos em ângulos θ tais que

d   s e n   θ = m d λ

Os máximos de difração e d a distância entre as fendas

e para interferência teremos

a   s e n   θ = m a λ

os mínimos, a a largura da fenda

A intensidade I para um ângulo θ é dada por

I θ = I m ( cos 2 ⁡ β )   s e n   α α 2

Onde

β = π d λ s e n   θ e α = π a λ s e n   θ

Passo 2

  1. Analisando o gráfico, temos que

    2. β s e n   θ = π d λ = 80   r a d → d = 80   r a d 435   n m π = 11,077   n m

    Passo 3

  2. Vamos tomar que

    3. m m a x = d λ s e n   θ m a x = d λ = 11,077   n m 435   n m ≈ 25,5

    Isso indica que temos 25 franjas laterais de um lado. Desta forma teremos 25 + 1 + 25 = 51

    Passo 4

  3. “Obviamente” o menor ângulo que existe um máximo é o máximo central, ou seja, θ = 0

    4. Passo 5

  4. Supondo que nenhum máximo seja totalmente eliminado por um mínimo, podemos supor que o máximo que pode existir um mínimo é em m = 25

θ = s e n - 1 m λ d = s e n - 1 25 435   n m 11,077   n m = 79,0 °

Resposta

  1. d =   11,077   n m
  2. 51 Franjas
  3. θ = 0
  4. θ = 79,0 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um experimento de dupla fenda, a distância entre as fendas é 5 m m e as fendas estão a 1 m de distância da tela. Duas figuras de interferência são vistas na tela, uma produzida por uma luz com um c
Na fig 35-37, as fontes AeB , emitem ondas de rádio de longo alcance com um comprimento de onda de 400 m , com a fase da onda emitida pela fonte A adiantada de 90 ° , em relação à onda emitida pela fo
Na fig 35-36, duas fontes pontuais isotrópicas, S 1 eS 2 , emitem ondas luminosas em fase cujo comprimento de onda é λ . As fontes estão sobre o eixo x , separadas por uma distância d , e um detector
Na fig 35-39 duas fontes pontuais isotrópicas, S 1 eS 2 , estão no eixo y , separadas por uma distância de 2,7 μ m , e emitem em fase com um comprimento de onda de 900 n m . Um detector de luz é coloc
Na Fig. 35-38, duas fontes pontuais isotrópicas, S 1 e S 2 , emitem luz em fase com comprimento de onda λ e a mesma ainplitude. As fontes, separadas por uma distância 2 d = 6,00 λ , estão em uma reta