Na Fig. 4-54, uma bola de massa de modelar descreve um movimento circular uniforme, com um raio de , na borda de uma roda que está girando no sentido anti-horário com um período de . A bola se desprende na posição correspondente a horas ( como se estivesse no mostrador de um relógio) e deixa a roda a uma altura acima do chão e a uma distância de uma parede. Em que altura a bola bate na parede?
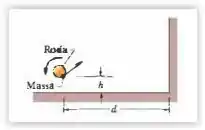
Passo 1
Então galera , separando as informações dadas pelo problema , temos que é a velocidade tangencial da bola e é o ângulo descrito pelo movimento em relação à horizontal. Nesse caso, usando a relação que já conhecemos , obtemos que :
O que significa que a bola bate na parede a uma altura de .
Resposta
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir