Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.2 - Ex. 13
A Fig. 13-37 mostra uma cavidade esférica no interior de uma esfera de chumbo de raio ; a superfície da cavidade passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera antes de ser criada a cavidade era . Com que força gravitacional a esfera de chumbo com cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros das esferas e o centro da cavidade?
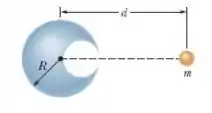
Passo 1
Show de bolinhas pessoal, esse problema a princípio pode parecer bem complicado, mas ele na verdade é bem mais simples do que parece.
Pense aqui comigo meu patrão. A região da esfera que foi removida não exerce gravidade sobre a massa , correto? Beleza. Mas isso não é a mesma coisa que considerar a esfera toda cheia exercendo gravidade sobre e uma esfera do tamanho da cavidade exercendo uma “gravidade negativa”? O efeito final será o mesmo.
Agora calcular o efeito de uma esfera com uma cavidade de pode ser bem complicado, mas calcular o efeito de uma esfera cheia e de outra esfera cheia com “gravidade negativa” é bem mais fácil. Esse é o pulo do gato pra resolver a questão.
Passo 2
Iradoso, então vamos começar determinando a massa que foi removida da esfera. A cavidade tem raio . Vamos chamar de a massa removida da esfera. Como a densidade do material é o mesmo, temos a relação:
Onde e representam a densidade da porção retirada da cavidade e a densidade da porção da esfera que permaneceu inalterada, respectivamente. Sendo assim:
Logo:
Passo 3
Belezoca, agora vamos considerar a influência gravitacional da esfera cheia e uma influência negativa de uma esfera de mesma massa da massa removida da esfera, ou seja, a massa virtual da cavidade. Temos então
Dessa maneira, substituindo os valores que o enunciado fornece pra gente, obtemos que:
Resposta
A força é de .