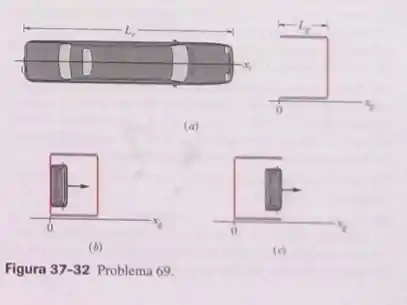
O problema do carro na garagem. Mário acaba de comprar a maior limusine do mundo, com um comprimento próprio . Na Fig. 37-32a, o carro aparece parado em frente a uma garagem cujo comprimento próprio é . A garagem possui uma porta na frente (que aparece aberta na figura) e uma porta nos fundos (que aparece fechada). A limusine é obviamente mais comprida que a garagem. Mesmo assim, Alfredo, que é o dono da garagem e conhece alguma coisa de mecânica relativística, aposta com Mário que é possível guardar a limusine na garagem com as duas portas fechadas. Mário, que parou de estudar física na escola antes de chegar à teoria da relatividade, afirma que isso é impossível, sejam quais forem as circunstâncias. Para analisar o plano de Alfredo, suponha que um eixo de referência , seja instalado no carro, com no para-choque traseiro, e que um eixo de referência , seja instalado na garagem, com na porta dianteira. Mário conduz a limusine em direção à porta da frente da garagem a uma velocidade de (o que na prática, naturalmente, é impossível). Mário está em repouso no referencial ; Alfredo está em repouso no referencial . Existem dois eventos a considerar. Evento 1: quando o para-choque traseiro passa pela porta da frente da garagem, a porta da frente é fechada. Vamos tomar o instante em que este evento ocorre como o instante inicial tanto para Mário como para Alfredo: . Este evento ocorre no ponto . A Fig. 37-32b mostra o evento 1 do ponto de vista de Alfredo (referencial ). Evento 2: quando o para-choque dianteiro chega à porta dos fundos da garagem, a porta é aberta. A Fig. 37-32c mostra o evento 2 do ponto de vista de Alfredo. De acordo com Alfredo. (a) qual é o comprimento da limusine? Quais são as coordenadas ( b) e (c) do evento 2? (d) por quanto tempo a limusine permanece no interior da garagem com as duas portas da garagem fechadas? Considere agora a situação do ponto de vista de Mário (referencial ). Nesse caso, é a garagem que passa pela limusine com uma velocidade de . De acordo com Mário, (e) qual é o comprimento da limusine? Quais são as coordenadas (f) e (g) do evento 2 (h) A limusine chega a passar algum tempo no interior da garagem com as duas portas fechadas? (i) Qual dos dois eventos acontece primeiro? (j) Faça um esboço dos eventos 1 e 2 do ponto de vista de Mário. (k) Existe uma relação causal entre os dois eventos, ou seja, um dos eventos é a causa do outro? (l) Finalmente, quem ganhou a aposta?
Passo 1
Para resolvermos esse problema vamos fazer uma análise da imagem e usar as relações para compressão do espaço e dilatação do tempo para cada referencial. Vamos precisar também lembrar dos postulados da relatividade e o conceito de simultaneidade para entender o fenômeno.
Passo 2
- Vamos começar chorando um pouco, pois esse enunciado é muito grande e me cansou muito escrever.... Não mais que resolver a questão, mas mesmo assim.
- Como o eixo não se move em relação a garagem, temos que (mesmo tamanho da garagem).
- Para , vemos na imagem que no instante a limusine tem o exato tamanho de , ainda sobrando uma distância para chegar a porta traseira. Podemos então dizer que o tempo que a limusine precisa para chegar a porta traseira será
- Como a limusine está no interior da garagem no intervalo , temos que o tempo de permanência será
- Para Mário, temos que a garagem que terá um tamanho inferior, assim, utilizando a mesma equação do item (a), temos que
- Como em relação a limusine o eixo está estacionário, temos que
- Da mesma forma que obtivemos a variação do tempo para a limusine em relação a garagem faremos para a garagem em relação a limusine. Utilizando a mesma relação, teremos que
- Para Mário não, isso seria impossível.
- Para Mário, o segundo evento ocorre primeiro.
- Para Mário, a garagem é muito curta em relação a limusine e o evento 2 acontece antes do evento 1. Isso explica o porquê ele consegue atravessar a garagem sem bater, diferente do ponto de vista do Alfredo, onde a limusine se torna menor que a garagem
- Não, já que o evento 1 poderia ter ocorrido nem necessariamente o 2 acontecer.
- Ambos estão corretos em cada referencial, mas se alguém merecia ganhar com certeza seria Mário, por ter coragem de ir a essa velocidade para entrar em uma garagem que claramente não era maior que o carro.
Bom, agora vamos lá! O problema inicia no referencial do Alfredo, logo vamos calcular o tamanho da limusine para Alfredo, que será dado pela seguinte equação
Passo 3
Passo 4
Então será
.
Passo 5
Passo 6
Passo 7
Passo 8
E será
Passo 9
Passo 10
Passo 11
Passo 12
Passo 9
Ps: Quem merecia ganhar também somos nós que fizemos esse exercício até aqui. Parabéns!