Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.2 - Ex. 29
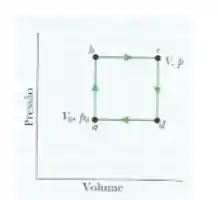
A figura abaixo mostra um ciclo reversível a que é submetido de um gás monoatômico ideal. Suponha que , , e . Calcule o trabalho realizando durante o ciclo, e energia adicionada na forma de calor durante o percurso e a eficiência do ciclo. Qual é a eficiência de uma máquina de Carnot operando entre a temperatura mais alta e mais baixa do ciclo? A eficiência calculada no ítem é maior ou menor do que a calculada no item ?
Passo 1
(a) Faala ae, beleza??
Entãao, sabemos qual é a fórmula do trabalho, certo? É essa aqui:
Ou seja, o trabalho pode ser calculado pela área do ciclo, dentro de um gráfico versus . Beleza?
Como nós temos um retângulo de lados e , a área vai ser e como o sentido é horário, o trabalho é positivo:
Substituindo os valores que temos:
Passo 2
(b) O calor adicionado pode ser dividido em dois processos: e . Vamos ao primeiro processo.
Vamos só lembrar da fórmulinha antes:
Então, com isso, achamos a temperatura por:
Precisamos determinar as temperaturas envolvidas.
Para o estado :
Para o estado :
Para o estado :
Passo 3
Agora vamos analisar cada processo.
O calor de é um calor específico a volume constante: , onde . Nesse caso, temos um gás monoatômico, então . Assim:
O calor de é um calor específico a pressão constante: , onde . Assim:
O calor total vai ser a soma deles:
Passo 4
(c) A eficiência desse ciclo vai ser:
E já calculamos esses dois caras:
Passo 5
(d) Para uma máquina de Carnot a eficiência seria:
Passo 6
(e) Maior, pois no (c) achamos e no (d) achamos .
Beleza?? Acabamos!