Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 107
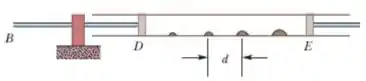
O método de Kundt para medir a velocidade do som. Na figura, uma barra está presa pela parte central; um disco na extremidade direita da barra está no interior de um tubo de vidro, cheio de gás, que também contém pedacinhos de cortiça. Existe um êmbolo na outra extremidade do tubo. A barra está acoplada a um vibrador mecânico que produz ondas longitudinais de frequência no interior do tubo, e a posição do êmbolo é ajustada para que seja criada uma onda estacionária. Quando a onda estacionária é criada, o movimento do gás faz com que os pedacinhos de cortiça formem pequenos montes nos pontos em que o deslocamento é nulo. Se e a distância entre montes vizinhos é , qual é a velocidade do som no gás?
Passo 1
A informação mais importante aqui é que os pedacinhos de cortiça formam montes nos pontos em que o deslocamento é nulo. Isso é importante porque assim podemos saber a posição dos nós!
A separação entre os nós equivale a meio comprimento de onda:
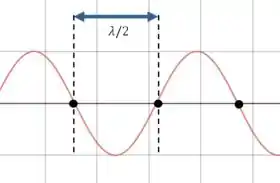
Então, se cada nó no desenho do enunciado está separado por uma distância :
Passo 2
Como podemos calcular a velocidade a partir disso?
Agora é só substituir os valores numéricos?
Resposta
A velocidade do som no gás é .