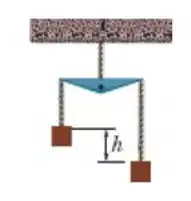
Na figura, dois blocos de mesma massa m = 2,00k g estão pendurados em cordas de comprimentos diferentes nas extremidades de uma balança situada na superfície da Terra. As cordas têm massa desprezível, e a diferença de comprimento entre as cordas é h = 5,00c m . Suponha que a Terra é esférica e homogênea, com massa específica ρ = 5,50g / c m 3 . Qual é a diferença de peso entre os blocos devido ao fato de um dos blocos estar mais próximo do centro da Terra do que o outro?

A diferença de peso seria de 3,07.10 - 7N .

Enunciado

Vamos começar encontrando a massa da Terra a partir da massa específica que foi dada no enunciado?

E precisamos usar a fórmula para o volume de uma esfera de raio :

Antes de substituir os valores, vamos converter para

E então:

Agora vamos analisar a força gravitacional que age sobre cada um dos blocos. Em geral, a força gravitacional é dada por:

Na superfície da Terra, temos , e queremos saber qual é a variação quando vamos para uma altura :

Vamos colocar em evidência:

Então:

Agora podemos expandir aquele termo entre parênteses por uma expansão binomial, mas tomando apenas os termos com potência menor do que :

Então, para :

Vamos substituir isso na fórmula de cima:

Agora vamos substituir a expressão que encontramos para :

E então:

A diferença de peso seria de .